0   引言

临近空间飞行器的发展已经成为目前国际上竞相争夺空间技术的焦点之一^[1-3]。自20世纪60年代以来的大量研究充分表明，推进系统与机体的一体化设计是实现高超声速飞行的关键，而推进系统与机体一体化的核心之一则是飞行器前体和进气道的一体化^[4]。高超声速进气道按照几何外形特征可主要分为二元进气道、轴对称外转折进气道、侧压式进气道以及三维内转进气道等几大类；而高超声速飞行器的前体则可分为翼身融合体、旋成体、升力体及乘波体等。

自Nonweiler^[5]首次提出楔导乘波理论以来，楔导乘波体已被广泛应用于高超声速飞行器的一体化设计中^[6-7]。Ferguson^[8]基于楔导乘波理论完成了整个推进系统与飞行器机体的一体化设计，该设计方法考虑了平面流动条件下的楔导乘波体与进气道的耦合问题。20世纪90年代，Sobieczky等^[9]提出了给定激波形状反求流场生成体的吻切乘波理论(Osculating Cone method)，拓展了乘波体的设计方法。基于此方法，Takashima等^[10]提出了能够实现外流乘波体与内流二维进气道耦合的一体化设计方法。在国内，尤延铖等进一步将外流乘波理论拓展至内收缩流动，提出了同时使用外流乘波体与内流三维内转进气道的双乘波一体化设计方案^[11-12]，解决了高超声速内外流的一体化设计问题。贺旭照^[13-14]与范晓樯^[15]等以前体/进气道一体化为研究对象，提出了各种类型的乘波进气道与前体的一体化设计方案，并通过试验研究与数值模拟给出了对应方案的气动特性。可以看到，目前国内外高超声速飞行器一体化的研究重心主要在乘波前体与进气道的匹配设计上。

然而，乘波前体在容积率、迎角特性及非设计点的工作性能方面存在一定缺陷。另一类曲锥前体构型因其结构简单、容积率大且迎角特性好等优点在飞行器机体和导弹布局中受到格外重视^[16-17]。国内外学者对曲锥前体构型的飞行器一体化设计也开展了大量的研究^[18-20]。但是，多数研究主要着眼于进气道的设计问题，并未研究曲锥前体与进气道之间的相互作用，尤其是捕获形状的选择与进气道基本流场的关系，以及迎角对进气道性能的影响等。针对此类问题，厦门大学的李怡庆等提出了一种曲锥前体/三维内转进气道的一体化设计方法^[21]，并着重分析了曲锥前体条件下进气道捕获形状的设计要素及其对此类一体化方案外形和性能的影响。

本文在文献[21]的基础上，着重探讨进气道侧壁外扩角这一影响因素对此类一体化构型气动性能的影响，设计了具有不同外扩角的两种一体化构型并开展了风洞试验研究。通过更换进气道唇罩部件实现进气道入口捕获形状以及压缩形式的转变，以期验证曲锥前体条件下进气道侧壁外扩角这一设计要素对一体化构型气动性能的影响。

1   曲锥前体/内转进气道一体化设计方法

文献[21]对曲锥前体的流动特征进行了详细的分析，认为对曲锥前体与三维内转进气道进行一体化设计时应将进气道靠近锥尖布置以达到有效利用曲锥前体的预压缩效果。同时，从提高一体化构型流量捕获特性的角度出发，进气道捕获形状(Flow Capture Tube, FCT)建议选用外扩构型以尽量避免一体化构型在迎角飞行状态下出现的侧壁横向溢流。这些要素在进行一体化设计时都需着重考虑。

曲锥前体与三维内转进气道一体化设计方法的主要步骤如下：

(1) 确定进气道捕获面积及捕获形状

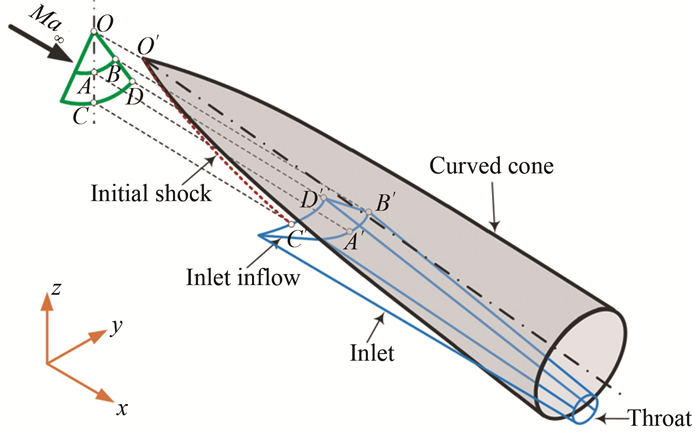
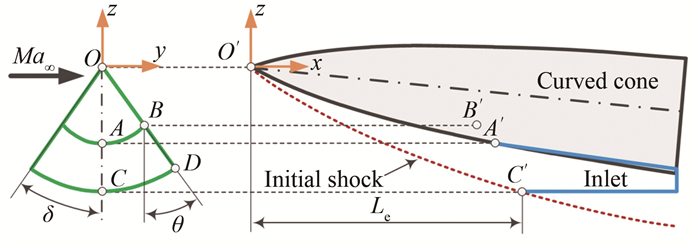
图 1给出了曲锥前体与三维内转进气道的几何布局形式，三维内转进气道位于曲锥前体的腹部。进气道的捕获形状由曲锥顶点O，进气道侧前缘点B，侧壁终点D以及进气道唇口点C决定。因此，将图 1中ODC所围区域定义为捕获形状(因捕获形状具有对称性，故取一半进行分析)。其中OBA所围区域代表由锥顶点至进气道入口的外压缩部分，而ABDC区域则表示由进气道入口到进气道出口的内压缩部分。进气道捕获面积由发动机流量需求确定，而捕获形状则主要根据三维内转进气道入口侧壁的外扩角θ、进气道捕获形状的圆心角δ和前体与进气道外压缩段总长度L_e确定，如图 1所示。通过合理的配置上述参数，即可确定进气道入口形状。

图  1  曲锥前体/内转进气道几何布局示意图

Fig.  1  Schematic of the curved fore-body and the inward turning inlet

下载: 全尺寸图片 幻灯片

(2) 设计进气道入口的三维形状

三维内转进气道的优点之一是在进气道入口产生的入射激波能够将入口完全封闭，流体无法穿越激波“泄露”到进气道外部，从而实现设计状态的全流量捕获。借鉴该思路，欲使进气道具有高流量捕获的特性，曲锥前体与三维内转进气道产生的入射激波应尽量封闭下游的内转进气道入口。

图 2给出了一体化设计时进气道入口形状的生成示意图。捕获形状的AB用以控制曲锥前体与进气道的连续过渡。因此将AB边沿流向水平投影至曲锥表面便可获得图 2中的三维形状A′B′，即为内转进气道的入口前缘型线。将C点沿流向投影至曲锥激波表面得到入口点C′，并且根据C′点和A′点的位置以及当地的平均马赫数确定三维内转进气道的入射内锥激波角。将BDC边的沿流向投影至三维内转激波面，便可获得内转进气道入口的三维侧壁形状B′D′C′。至此，一体化过程中内转进气道的三维入口形状A′B′D′C′便已确定，如图 2所示。

图  2  内转进气道入口形状设计

Fig.  2  Design of the inlet capture shape

下载: 全尺寸图片 幻灯片

(3) 根据进气道入口三维形状及位置，生成三维内收缩基本流场，得到进气道压缩型面

根据圆锥母线构型及三维内转进气道入口位置，确定基本流场入口条件。本文取进气道入口处的平均马赫数作为基准流场入口马赫数。根据上文得到的三维内转进气道入射内锥激波角可得到基准流场。以进气道入口形状为基础，在基准流场中进行流线追踪并于反射激波处截断，便可得到与曲锥前体匹配良好的三维内转进气道构型。

2   锥前体/内转进气道一体化构型试验与数值方法

2.1   一体化试验模型设计

如上所述，针对此类一体化构型，进气道捕获形状的设计主要由三维内转进气道入口侧壁的外扩角θ、进气道捕获形状的圆心角δ、前体与进气道外压缩段总长度L_e、侧壁前缘点位置4个要素决定，其中入口侧壁的外扩角对整体性能的影响尤为显著。因此，本文专门针对不同的进气道侧壁外扩角展开风洞试验研究。

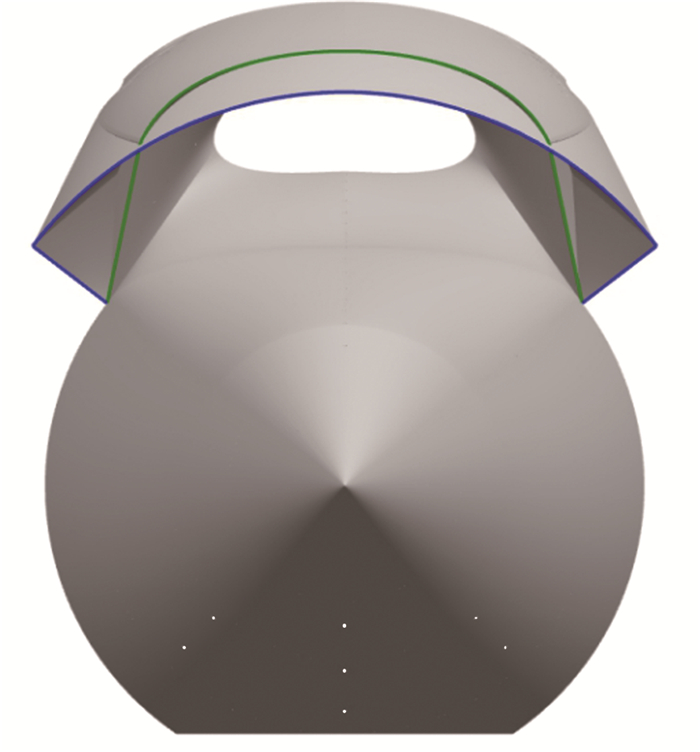
在来流马赫数Ma=6.0，迎角α=0°条件下，设计了两套曲锥前体与三维内转进气道一体化风洞试验模型, 如图 3所示。两模型均选择内收缩锥基本流场的下半区布局入口形状，且具有相同的曲锥前体，仅通过更换唇罩部件实现进气道捕获形状与压缩形式之间的转变。如图 4所示, 绿色实线代表模型1唇罩形状，蓝色实线代表模型2唇罩形状。可以看到，模型2具有明显的外扩构型，而模型1唇口侧壁的外扩角略小于零。为有效比较两模型之间的差别，在设计之初保证两模型具有基本相同的总收缩比、内收缩比以及捕获面积。表 1给出了两模型的唇口形状设计参数，其中TCR代表试验模型的总收缩比，ICR代表模型的内收缩比，A_c代表模型的捕获面积。需要说明的是，本文设计的试验模型由于采用内收缩锥下半区进行流线追踪，因此D′点位于B′点上游。相较D′点位于B′点下游而言，该方案在相同流量捕获的情况下迎风面积更小，有助于降低一体化构型的阻力。

图  3  曲锥前体/内转进气道一体化试验模型

Fig.  3  Schematic of two test models

下载: 全尺寸图片 幻灯片

图  4  两试验模型的唇罩形状示意图

Fig.  4  Inlet lip shapes of two test models

下载: 全尺寸图片 幻灯片

表  1  试验模型1、2的设计参数

Table  1  Design parameters of two models

	δ/(°)	θ/(°)	Le/m	TCR	ICR	Ac/m2
模型1	52.48	-11.77	0.518	6.0	2.95	0.01302
模型2	52.48	52.48	0.470	6.0	2.97	0.01297

下载: 导出CSV 

| 显示表格

试验模型的测点均通过联通管道将气流引入曲锥前体内部进行测量。通过以上设计，能够将静压测量系统完全布置于曲锥前体之内，无需在模型外侧布置静压测量腔，在最大程度上实现了保型设计。需要特别指出的是，由于模型设计时考虑唇罩的可更换性，本文将进气道唇罩与曲锥前体采用螺纹连接，当需要更换部件时，仅需拆卸唇罩部位即可。图 5给出了试验模型的拆解示意图。

图  5  曲锥前体/内转进气道一体化试验模型拆解图

Fig.  5  Exploded schematic of test model

下载: 全尺寸图片 幻灯片

图 6给出了曲锥前体/内转进气道一体化试验模型的装配图。试验模型总长1675 mm，其中曲锥前体加内转进气道部分长度为900 mm。考虑到进气道出口为腰型，而下游反压调节装置需要一个圆形入口。本文在进气道下游设计了一段过渡段，该过渡段总长240 mm，出口为直径75 mm的正圆。过渡段后连接长径比为7、直径为75 mm的等直圆柱段，在等直圆柱段的出口设置反压调节锥以改变下游的反压，模拟进气道出口条件。

图  6  一体化试验模型装配图

Fig.  6  Assembled schematic of test model

下载: 全尺寸图片 幻灯片

2.2   风洞试验设备

本文试验在中国空气动力研究与发展中心高超声速空气动力研究所的脉冲燃烧风洞中完成。该风洞喷管出口直径为600 mm，采用烧氢补氧的方式来获取高的来流总焓。马赫数为6时，来流总压为4.8 MPa，来流总温为1480 K。风洞的有效工作时间大于300 ms。为延长试验时间并扩大均匀区范围，在试验模型之外额外安装了扩压器装置，经延长后的有效时间大于400 ms。在风洞内安装时，在各个迎角状态下，模型前缘锥点(O′)至唇口点(C′)连线的中点在高度方向上应与喷管中心重合，最大程度保证进入进气道内部气流的均匀性。试验过程中采用纹影设备对流场状态进行显示，相机分辨率为1024 pixel×1024 pixel，帧频为4000 fps，纹影窗口显示范围为300 mm，选取进气道唇口附近流场进行拍摄。图 7给出了模型照片以及安装在风洞中的相对位置。本文在该风洞中对两试验模型分别在通流状态及加反压条件下进行测试，以验证一体化设计方法的可行性并探讨外扩角对进气道性能的影响。

图  7  风洞试验中试验模型安装位置示意图

Fig.  7  Schematic of installation position of the test model in the wind tunnel

下载: 全尺寸图片 幻灯片

试验过程中采集的参数主要包括：沿程静压、进气道出口截面静压、皮托压和进气道流量。其中，沿程静压测点分别布置在曲锥前体的上、下壁面，进气道的上、下壁面以及侧壁。由于曲锥弹身与进气道为一体化设计，为准确描述，下文将曲锥弹身上壁面与进气道下壁面称为压缩侧，进气道上壁面称为唇罩侧，进气道侧壁称为侧壁面。试验中数据采样长度为3 s，覆盖整个试验过程，采样频率为40 kHz。图 8给出了某次试验的风洞后室总压、进气道内壁面测点以及进气道出口皮托压信号随时间的变化曲线，横坐标单位为s。可以看出，模型各点动态信号与风洞后室基本同步，表明测试系统的响应速率是足够的。从图中还能看出，该次试验有效数据时间段大于300 ms。

图  8  典型测点动态压力信号时间历程

Fig.  8  Dynamic pressure signal at typical measuring point

下载: 全尺寸图片 幻灯片

2.3   数值模拟计算条件与网格

为更加准确地分析试验模型的三维流动特征, 本文还对两试验模型在设计状态下进行了全粘的数值模拟。计算软件采用商用CFD软件ANSYS Fluent。选用的湍流模型为SST k-w模型，方程的离散选择二阶迎风格式，通量类型选择AUSM格式。分子粘性系数采用Surtherland公式计算。计算过程中假设流体为量热完全气体，壁面为绝热、无滑移、固体边界。

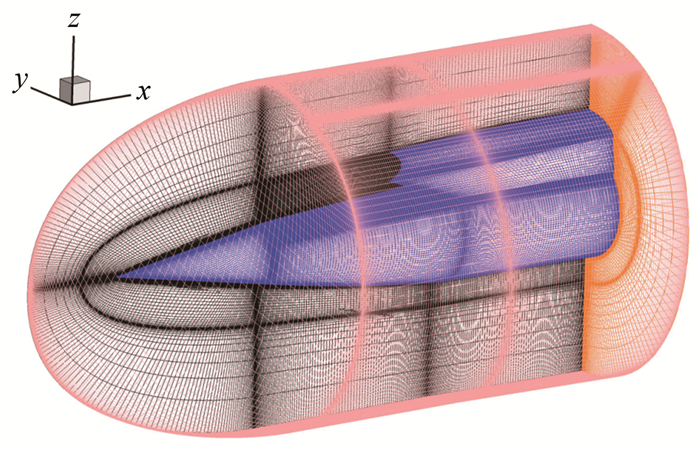
鉴于试验模型的对称性，仅采用半模进行数值仿真。图 9给出了试验模型1的网格结构，模型2与之类似。其中，蓝色网格部分边界条件设置为无滑移绝热壁面，黑色网格设置为对称面边界，粉色网格为压力远场，而橙色网格则设置为压力出口边界。两模型总网格数均为500万左右。对近壁面网格进行了等比加密处理，近壁面y⁺小于10。由于一体化构型三维造型的复杂性，对生成的网格进行了全局正交性优化。此外，为了提高激波形状的捕获精度，对网格进行了自适应处理。

图  9  试验模型1网格结构图

Fig.  9  Mesh distribution of model 1

下载: 全尺寸图片 幻灯片

3   曲锥前体/内转进气道一体化模型试验及数值结果对比

3.1   通流状态对比分析

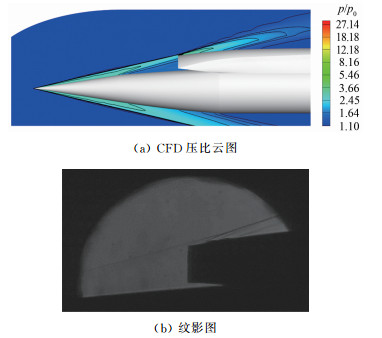
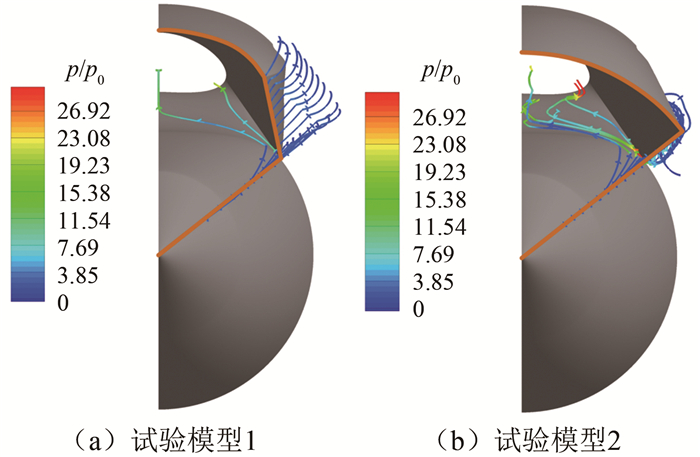
本文在设计通流工况(Ma=6.0, α=0°)下，提取两试验模型数值模拟结果对称面激波形态与纹影结果进行对比，如图 10和11所示(p₀为来流静压)。可以发现，在该试验工况下，试验结果基本还原了预期的波系结构，前缘产生的入射激波汇于进气道唇口位置，最大程度抑制了唇罩侧的溢流，也证明了该一体化设计方法的可行性。

图  10  设计通流状态下试验模型1对称面激波形态

Fig.  10  Shock wave on the symmetry plane of model 1 under design conditions

下载: 全尺寸图片 幻灯片

图  11  设计通流状态下试验模型2对称面激波形态

Fig.  11  Shock wave in the symmetry plane of model 2 under design conditions

下载: 全尺寸图片 幻灯片

值得注意的是，由于前缘激波为圆锥激波，因此仅能保证三维激波将进气道唇口封闭，在侧壁处不可避免会存在横侧向溢流。由于纹影设备仅能获取对称面内的激波形态，无论前体激波或后体激波，试验结果与数值模拟结果均基本吻合，因此本文利用数值模拟结果进一步分析模型的三维流动特征。图 12为两试验模型的局部流线示意图，图中橙色实线代表模型的理论捕获形状。可以看到，对于试验模型1，由于进气道侧壁不具有外扩角，经过前缘激波压缩后的流线出现偏折，进气道侧壁未能实现有效的流量捕获; 而对于试验模型2，外扩的进气道侧壁构型能够很好地减弱横向溢流损失，因此，试验模型2具有相对较好的流量捕获能力，这在后续的试验结果中可以得到进一步验证。

图  12  试验模型流线示意图

Fig.  12  Streamlines distribution of two test models

下载: 全尺寸图片 幻灯片

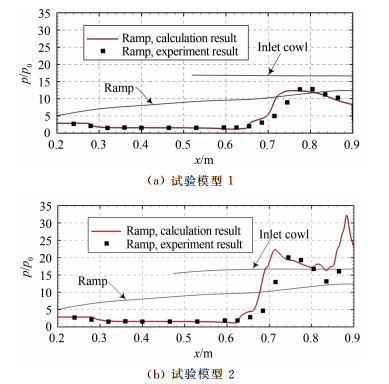
图 13给出了2套模型在设计通流状态下压缩侧的沿程静压比的试验与数值对比，其中灰色细实线为试验模型压缩侧及唇罩侧的构型曲线。可以看到，数值模拟的结果与试验结果基本吻合。同时，对比两模型数据可以发现，两模型在x=0.6 m至x=0.7 m之间出现压力抬升，且模型2的压力突变位置相对于模型1更靠近流场上游，这是由于模型2进气道入口侧壁外扩，导致侧壁产生了较强的压缩效果，该压缩向对称面处汇聚，使得流场压力突变位置提前。此外，两模型在压缩侧的压力分布均呈现出阶梯式的上升规律，结合图 14的对称面流场马赫数分布可以发现，该阶梯的第一级压升由边界层分离产生的诱导激波引起，第二级压升则由唇口反射激波与边界层再附激波共同作用产生。其中，模型2由于压缩侧分离诱导激波较强且反射激波提前，因此其壁面下游沿程压比的峰值达到模型1的2倍以上。

图  13  设计通流状态下试验模型压缩侧沿程压力分布对比

Fig.  13  Pressure ratio on the ramp surfaces of two test models under design conditions

下载: 全尺寸图片 幻灯片

图  14  试验模型对称面马赫数云图

Fig.  14  Mach number contours on the symmetry plane of two test models

下载: 全尺寸图片 幻灯片

同时，图 14分离包内的二次流线图说明两试验模型的分离流动并未沿流向产生持续发展的涡流结构，而主要表现为由两侧向对称面汇聚的特征，且模型2强于模型1。因此，图 15进一步提取了两模型内流通道不同特征截面的流动特征进行分析。可以发现，试验模型1周向反射激波强度基本相同，具有较好的三维压缩特征，经过激波压缩后，波后马赫数较为均匀；而试验模型2两侧激波强度显著强于唇口反射激波强度，侧压特征较为明显，这就导致试验模型2两侧气流向对称面汇聚的趋势更加强烈，形成图 14(b)中的流线上洗效应。此外，两模型的低能流区域都集中于对称面中心位置，因此，虽然两模型都出现了面积较大的低能流区域，但整个内流通道仍然具有较大的流通面积，并未严重影响进气道的起动及性能。

图  15  两模型的横截面流场特征对比

Fig.  15  Slice comparison of flow characteristics of two test models

下载: 全尺寸图片 幻灯片

3.2   反压特性对比分析

除了通流情况下的高超声速进气道性能之外，决定进气道能否与燃烧室匹配工作的另一重要的性能指标是反压特性，尤其是最大抗反压能力。在高焓风洞试验中，本文采取调节出口堵锥位置的方式，分别模拟了两套试验模型进气道下游的反压条件，同时采集了测量截面的皮托压、壁面静压以及扩张段与流量筒壁面沿程静压分布。此外，通过间接测量的方法获得了进气道流量捕获系数。本试验针对两模型分别在设计工况(Ma=6.0，α=0°)下进行了3次锥位调整。堵塞度定义为堵锥喉道处面积与等直流量筒截面积之比，即0%堵塞度表示流量筒出口处于完全开启，而100%堵塞度则表示出口完全堵死。图 16给出了两试验模型反压状态下压缩侧沿程静压分布规律。随堵塞度的增加，出口截面压强不断升高，沿程壁面静压受扰动的流向位置不断前移。图中黑色虚线表示最大反压状态，橙色虚线表示反压不起动状态，而灰色细实线为试验模型压缩侧及唇罩侧的构型曲线。

图  16  反压条件下试验模型压缩侧沿程压力分布对比

Fig.  16  Pressure ratio on the ramp surfaces of two test models under back-pressure conditions

下载: 全尺寸图片 幻灯片

从图中可以发现，试验模型2在堵塞度为16%时内流通道中尚未产生激波串流动(见图 16(b))，而当堵塞度增加至20%时，压缩侧在第23号壁面测点位置出现压力突变，而压力突变之前的沿程静压分布与堵塞度16%时基本重合，因此可判定，该堵塞度情况下激波位于第23测点附近，此时激波串位于进气道喉道下游，尚未进入进气道内流通道；当堵塞度增加至21%时，压力扰动前传至第6号壁面测点，可以看到，该测点已位于进气道入口之前，此时进气道不起动。因此，试验模型2在设计状态(Ma=6.0，α=0°)下，堵塞度为20%的状态对应其最大反压状态，此时进气道承受反压为53.03倍来流静压。若继续增加反压，进气道将出现周期性的“喘振”，无法稳定工作。

反观试验模型1在不同堵塞度情况下的壁面压力分布曲线(见图 16(a))，抗反压能力却有显著的不同。在堵塞度20%时，流道内激波串已前传至第20测点附近，而该测点上游的流场未受到影响，此时出口反压达到来流静压的55.89倍，超过试验模型2的最大反压状态。堵塞度进一步增大，出口反压也随之增加，当堵塞度增加至39%时，出口反压高达来流静压的139.01倍，此时，壁面静压受扰动的流向位置前移至第15测点，该测点位于进气道喉道截面上游，测点之前流场未受扰动，测点之后压力持续升高，进气道仍处于起动状态，但反压已对进气道喉道之前的内部流场产生了影响；进一步将出口堵塞度增大至57%，压力脉动迅速前传至第7测点，该测点位于进气道唇口附近，进气道出现“喘振”的不起动现象。

综上所述，在本文设计条件下，虽然外扩构型有助于提高此类一体化构型进气道的流量捕获能力，但从其最大抗反压能力的角度出发，具有三维周向等强度压缩特点的内流通道能够更好地拓宽一体化构型的工作范围。从试验结果来看，试验模型2相对于模型1具有更大的压缩量，而增压比的提高有助于进气道抗反压能力的提高，但根据试验结果可以很明显地发现试验模型1抗反压能力较大。可见，流场均匀性对整体构型的抗反压能力产生了主要影响，该特征在设计过程中应着重考虑。

3.3   性能参数对比分析

通过调节出口堵塞度，最终获得了测量截面的皮托压与壁面压力试验数据，进而可获得进气道在各状态下的流量捕获系数Φ，如表 2所示。前文结合试验纹影与数值模拟结果获得的三维流场结构已简要说明了两类一体化构型在流量捕获能力方面存在的差别，表 2中显示的数据进一步验证了该结论的正确性。对比两试验模型可以看出，除不起动状态外，试验模型2在各状态下的流量捕获系数均高于0.95，这正是因为进气道侧壁外扩带来的优势。而前文分析中发现，较大的侧壁外扩角对进气道内部流场的组织是不利的，试验模型1因其三维周向压缩的特点(图 15)，在内流通道中具有更均匀的流场结构，该流动特征对提升一体化构型的起动与抗反压能力均起到积极作用。

表  2  试验模型1、2流量捕获系数对比

Table  2  Mass flow rate ratio of two test models

	Start condition	Max back-pressure condition	Unstart condition
试验模型1	0.819	0.821	0.366
试验模型2	0.959	0.963	0.496

下载: 导出CSV 

| 显示表格

表 3和4进一步给出了两套试验模型的抗反压能力与喉道性能的对比。其中，p₀代表来流静压，p/p₀代表出口截面压比，p_throat/p₀代表喉道截面压比，p_{throat, t}/p_{0, t}代表喉道截面与来流的总压比。针对抗反压性能，试验模型1表现出明显优于模型2的特征，最大抗反压能力达到135.91倍的来流静压，而模型2仅能抵抗下游53.03倍的来流静压。此外，两模型的喉道性能存在较大差别。试验模型2因其较强的侧压特征，将马赫数6.0的高超声速来流压缩至2.44，且由于较紊乱的内流特征(图 15)，导致喉道总压恢复系数仅为0.357；而试验模型1在相同工况下则具有0.523的总压恢复系数，喉道马赫数为2.93。根据前文所述，两模型具有相同的总收缩比与内收缩比，可以发现不同的入口形式与压缩形式对进气道整体气动性能产生了显著的影响。因此，在设计曲锥前体进气道一体化构型时必须着重考虑其流量捕获能力与出口气动性能之间的相互关系，尽量综合两者之间的相互影响。

表  3  试验模型1、2抗反压能力对比

Table  3  Back-pressure performance of two test models

	Start condition	Max back-pressure condition	Unstart condition
试验模型1	55.89	135.91	54.25
试验模型2	19.18	53.03	38.88

下载: 导出CSV 

| 显示表格

表  4  试验模型1、2喉道性能对比

Table  4  Throat performance of two test models

	Mathroat	pthroat/p0	pthroat, t/p0, t
试验模型1	2.93	19.44	0.523
试验模型2	2.44	29.08	0.357

下载: 导出CSV 

| 显示表格

4   结论

本文介绍了具有高流量捕获能力的曲锥前体与三维内转进气道一体化的设计方法。针对进气道侧壁外扩角这一设计因素，设计了具有不同捕获形状的两种一体化构型，并完成了两类模型在设计状态下的风洞试验及计算对比研究。得出如下结论：

(1) 曲锥前缘产生的初始入射激波在设计通流状态下能够很好封闭进气道唇罩，进而起到抑制唇罩溢流和提高一体化构型流量捕获能力的效果。同时，通流状态下，风洞试验获得的一体化构型压缩侧的沿程压力分布与数值模拟的结果基本吻合，体现了该类一体化设计方法的可靠性。

(2) 受下壁面气流分离影响，试验模型2抗反压能力小于试验模型1，最大反压分别为53.03与139.01倍来流静压。

(3) 对比两试验模型的流量捕获特性，试验模型2在各反压状态下的流量捕获系数均高于0.95，而试验模型1最大流量捕获系数为0.821。

(4) 此类一体化构型外扩角的增加，在提高流量捕获的同时削弱了构型的抗反压能力及进气道出口性能。因此，设计此类一体化构型时，需要兼顾外扩角对一体化构型流量捕获及出口性能的影响，选择合适的外扩角以生成符合需求的一体化设计方案。