Experimental and theoretical model study on effective thermal conductivity of SOFC porous electrode
-
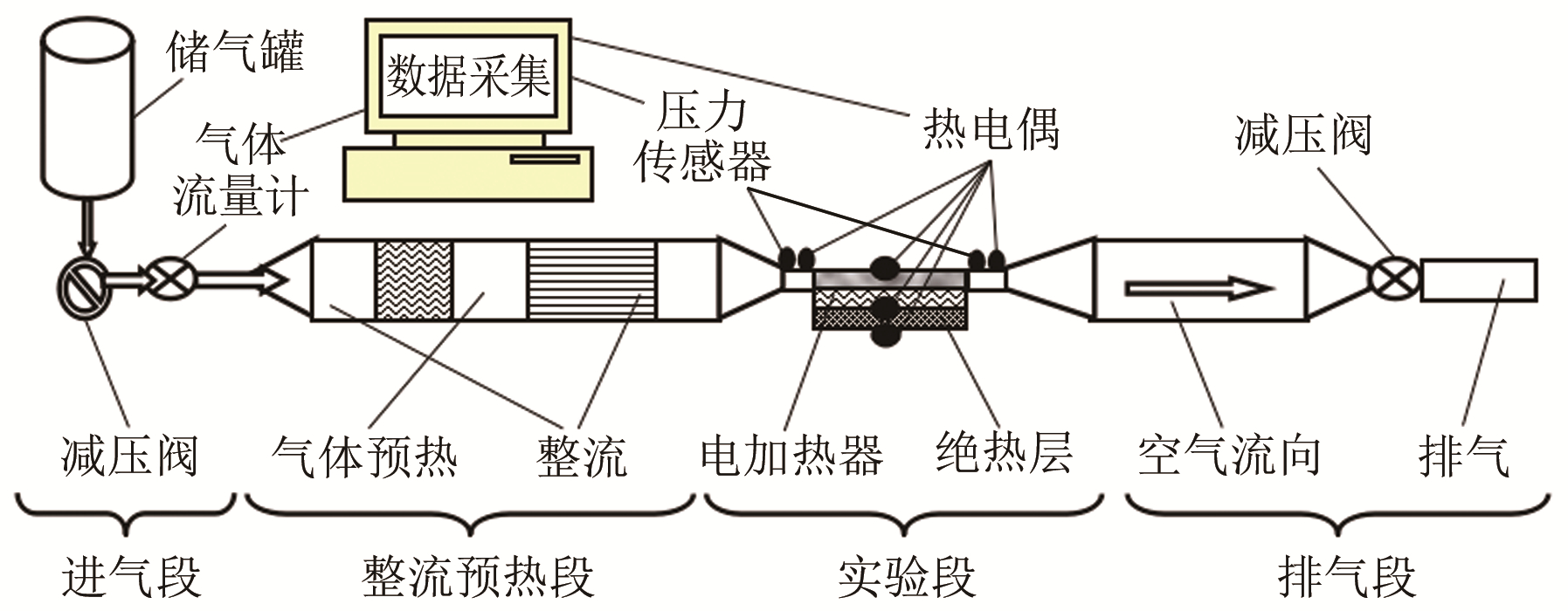
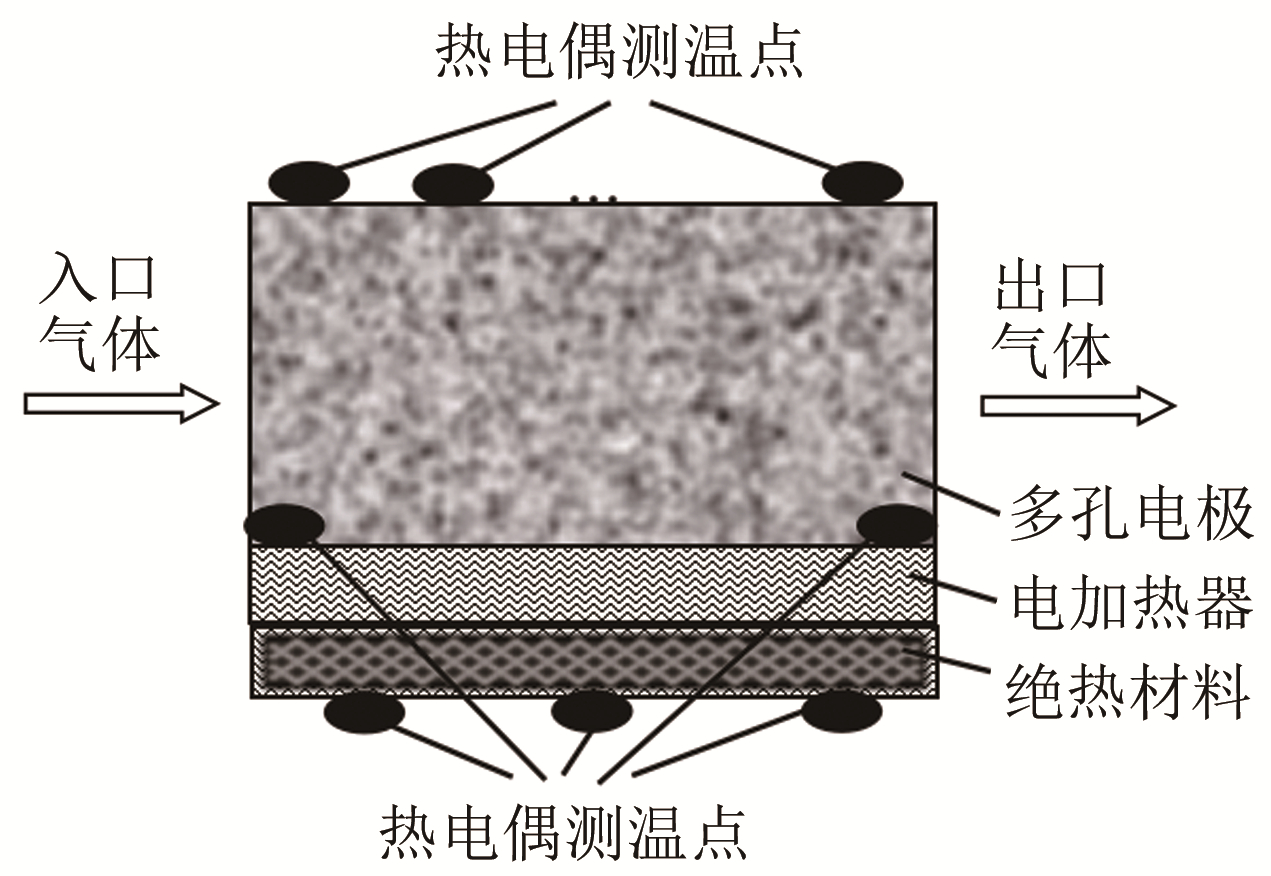
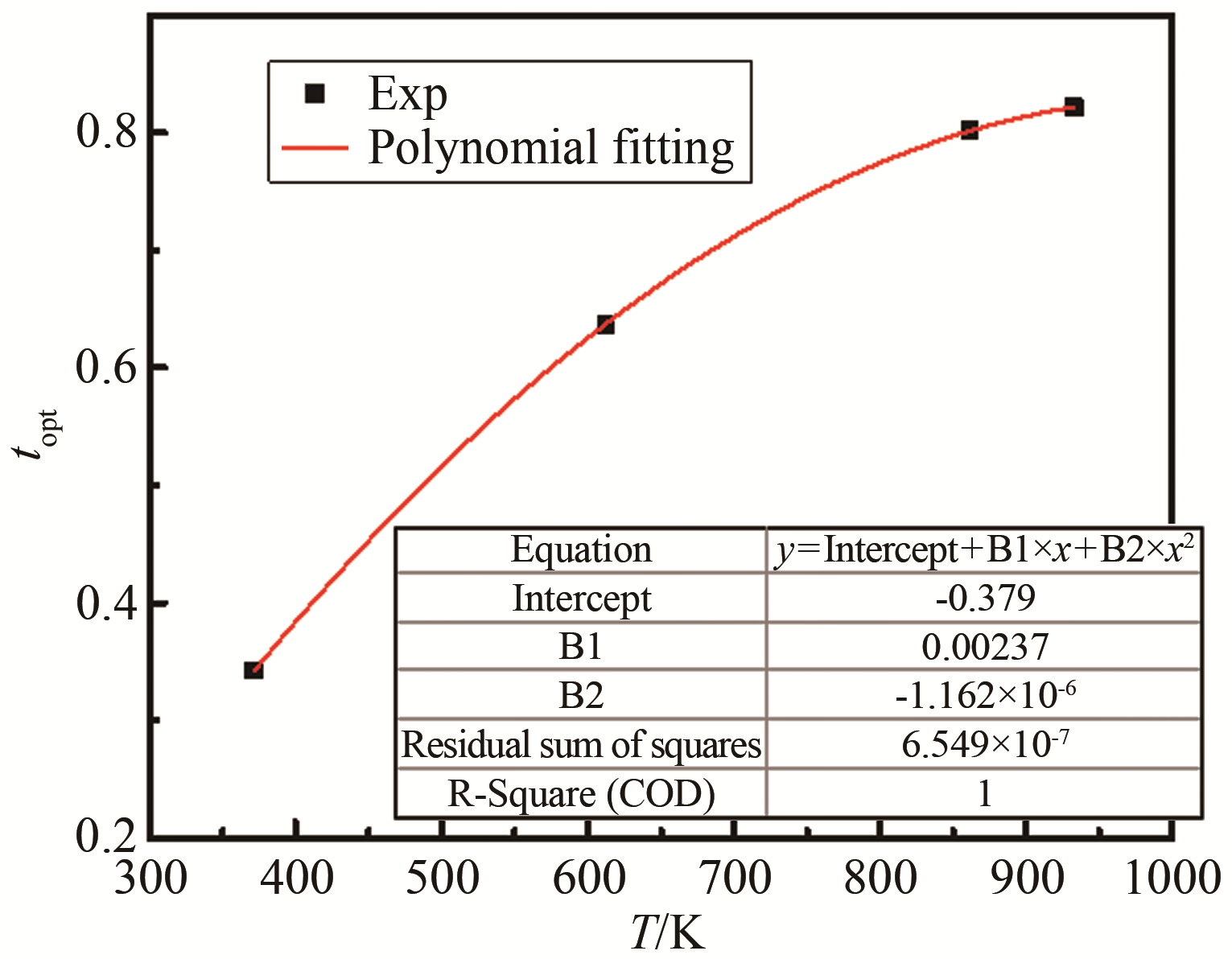
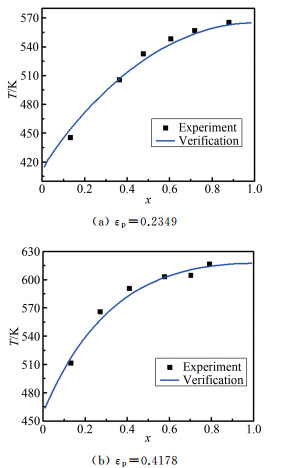
摘要: 固体氧化物燃料电池(SOFC)内部流动传热和化学反应复杂,容易产生热不平衡区。获取高精度的多孔电极有效导热系数对于建立多物理场耦合数值分析模型和电池热管理具有重要的意义。基于稳态法设计并搭建了多孔材料有效导热系统实验平台和测量系统,在372.1~932.4 K温度范围内详细测量了多孔电极实验样件温度分布,通过多孔材料内传热理论分析,基于现有EMT和ME1数学模型,利用比例因子t构造了温度修正的SOFC多孔电极综合有效导热系数的计算模型。同时通过对比孔隙率为0.2349~0.4178的3个实验样件表面温度的计算值和实验测量值,验证了该有效导热系数模型的有效性和高精度。Abstract: The flow heat transfer and chemical reaction inside the Solid Oxide Fuel Cell (SOFC) are complex, and it is easy to generate thermal imbalance zones. Obtaining high-precision effective thermal conductivity of porous electrodes is of great significance for the establishment of numerical analysis models of multi-physics field coupling and the thermal management. In this paper, an experimental platform and measurement system for the effective heat conduction system of porous materials was designed and constructed, which is based on the steady-state method. The temperature distribution of the porous electrode test specimens was measured in detail in the temperature range of 372.1~932.4K. Through the theoretical analysis of heat transfer in porous materials, the calculation model of the comprehensive effective thermal conductivity of temperature-corrected SOFC porous electrodes was constructed using the scale factor t, which combines the existing EMT and ME1 mathematical models. In addition, the validity and high precision of the effective thermal conductivity model were verified by comparing the calculated values with the experimental measurements of the surface temperatures of the three test specimens with the porosity of 0.2349~0.4178.
-
Keywords:
- SOFC /
- porous electrode /
- effective thermal conductivity /
- porous model
-
0 引言
常规高超声速风洞是以纯净空气为工作介质和以对流方式加热的高超声速风洞,是高超声速飞行器研制必备的试验设备。20世纪50年代,为了满足高超声速飞行器研制需要,人们开始建造常规高超声速风洞,自此以后,随着高超声速飞行器的不断发展,常规高超声速风洞一直处于改造和建设之中,设备的规模越来越大。以风洞喷管的出口尺寸计,常规高超声速风洞从最初的200~300mm量级,主要解决弹头等简单飞行器外形的气动研究和验证问题;发展到500~700mm量级,主要解决飞船等带表面凸起的飞行器外形的气动研究和验证问题;再发展到目前的1000~1200mm量级,可解决航天飞机等较复杂飞行器外形的气动研究和验证问题[1-2]。展望今后高超声速飞行器的发展,美国已经对2400~3000mm量级常规高超声速风洞提出建设需求[3]。
但是,随着风洞尺寸的增加,风洞运行所耗费的能源迅速增加[4]。以常规高超声速风洞在马赫数5至8时所需的加热功率为例,不同尺寸的风洞所需加热功率为:500~700mm量级,所需加热功率约6~8MW;1000~1200mm量级,所需加热功率约40~50MW;2400~3000mm量级,所需加热功率约250~320MW。
如何在满足高超声速飞行器试验对风洞尺寸要求的条件下,节省风洞运行时的能量消耗,已成为常规高超声速风洞设计技术发展必须考虑的重要问题。针对这个问题,本文从常规高超声速风洞的气动布局角度进行了初步探索。首先总结现有常规高超声速风洞的气动布局;在此基础上,对常规高超声速风洞中的能量运行特点,以及不同布局中工作气体余热的处理情况进行分析;然后,结合常规高超声速风洞的运行特点,分析风洞中可能采用的余热利用技术;最后,提出一种基于余热利用的常规高超声速风洞布局方案,并对该方案中的各种关键问题进行讨论。
1 现有常规高超声速风洞的气动布局
按照常规高超声速风洞的运行方式,风洞的气动总体布局分成3类,第一类是暂冲式,第二类是连续式,第三类是暂冲-连续混合式。3类常规高超声速风洞的气动总体布局各有其特点,在实际建成的风洞中均有应用。迄今为止,绝大多数常规高超声速风洞,无论尺度大小,功能如何,采用的大多是暂冲式气动布局;采用连续式气动布局的风洞较少,最典型的是美国AEDC的B、C风洞[5-7];采用暂冲-连续混合式气动布局的常规高超声速风洞更少,最典型的是美国Langley的1251A风洞。现将3类气动布局的形式总结如下[8-10]。
1.1 暂冲式气动布局
常规高超声速风洞的暂冲式布局也有3种形式:引射式、真空式以及引射-真空混合式。典型的引射式布局形式和真空式布局形式的示意图如图 1和2所示。
为了获得更宽的马赫数、雷诺数模拟范围,常规高超声速风洞还可采用引射-真空混合式布局,如图 3所示。
暂冲式常规高超声速风洞的运行方式是气罐中的压缩空气经过加热系统后达到所需的温度,然后通过型面喷管,在试验段形成试验所需的高超声速流场,最后经由超声速扩散段升压后进入引射排气系统,排入大气,或经过冷却器进入真空系统,然后由真空泵系统排入大气。
1.2 连续式气动布局
典型的连续式布局的示意图如图 4所示。
连续式常规高超声速风洞的运行方式是:封闭管路系统中一定密度的空气经过压缩机系统升压,再经过加热系统升温,达到建立流场所需的压力和温度,然后通过型面喷管,在试验段形成试验所需马赫数的流场;完成试验功能的气流经由超声速扩散段初步升压后,进入冷却器,降温后由真空系统进一步升压,进入压缩机系统,经历下一个循环。
1.3 暂冲-连续混合式气动布局
暂冲-连续混合式气动布局常规高超声速风洞,结合了连续式常规高超声速风洞和真空布局的暂冲式常规高超声速风洞的特点,可以模拟的飞行高度更高,相应的雷诺数范围更大,可达到的马赫数更大。
Langley的1251A风洞就采用了这种布局方案,其示意图如图 5所示。
暂冲-连续混合式常规高超声速风洞的运行方式是,通过关、启相应支路上的阀门,风洞既可以按连续式常规高超声速风洞的方式运行,也可以按真空布局的暂冲式常规高超声速风洞的方式运行。
2 现有常规高超声速风洞的能量运行分析
在常规高超声速风洞运行过程中,是否存在可节省的能量,需要从常规高超声速风洞中能量流通的过程来分析。
常规高超声速风洞的运行过程可近似用理想气体的一维流动理论来描述。根据此理论,一定流量的空气,在常规高超声速风洞喷管出口形成所需马赫数的流场,需要2种能量,压力势能和热能;2种能量分别由压缩机系统和加热器系统提供,如图 6所示。
经过常规高超声速风洞喷管后,气体中2种能量大部分转化为气体的动能。根据理想气体的一维流动理论,喷管内的流动为一维等熵流动,喷管仅起能量转化的作用,而进入喷管的气体总能量与喷管出口的气体总能量相等。
在试验段内,由于激波的作用,气体损失掉大部分的势能,而热能未损失。流出试验段后,气体完成了试验功能,成为废气,排入超扩段,而废气包含着未损失的热能。风洞运行中气流能量的主要变化过程如图 6所示。
上述分析给出了常规高超声速风洞所有气动布局共同的能量运行特点:风洞运行需要热能,但基本不损耗热能;风洞的废气包含着未损失的热能。但是,各气动布局的能量运行又有各自不同的特点,主要表现在各气动布局对于废气中热能的处理上。在暂冲-引射式气动布局中,超扩段中废气的热能,随废气通过亚扩段和消音塔直接排入大气中;在暂冲-真空式气动布局中,超扩段中废气进入冷却器,废气的热能通过冷却器全部消耗掉,废气再经真空系统排入大气;在连续式气动布局中,超扩段中废气先进入冷却器,废气的热能通过冷却器全部消耗掉,然后废气被增压回收,循环利用。后2种布局不回收废气中的热能,还要再损失冷却器运行所需的能量。
上述分析基于理想流体的理论,未考虑气体沿程的热损失;实际风洞运行中,气体沿程的热损失是确实存在的。根据边界层理论,可以初步估计出废气中包含的热能,其值约为气体总加热量的80%。
3种典型气动布局的热能损失位置及量级如表 1所示,表中还给出了运行冷却器消耗热能时的附加能量损失的量级。能量的量级用热能损失的量占气体被加热的总热量百分比表示。
表 1 3种典型布局的热能损失位置及量级Table 1 Location and magnitude of thermal losses in three typical layouts
沿程
损失排空
损失冷却
损失附加
损失暂冲-引射式 20% 80% 0 0 暂冲-真空式 20% 0 80% 5% 连续式 20% 0 80% 5% 3 大尺度常规高超声速风洞的节能气动布局
由上节的分析可知,现有的常规高超声速风洞的气动布局均未进行剩余热量回收。为了降低新建大尺度常规高超声速风洞的运行成本,在设计和建设前,需要研究常规高超声速风洞的剩余能量回收技术,并将之应用于风洞气动布局中,找到适合大尺寸常规高超声速风洞的新型布局。
3.1 常规高超声速风洞的剩余热能的回收形式
到目前为止,现有的常规高超声速风洞设计中从未考虑过剩余热能的回收问题,无经验可利用。这个问题的解决需要借助工业上余热回收的做法。工业上余热回收有3种方法[11],一是用蓄热材料回收,二是转化为其他能量形式,三是换热回收。3种方法各有特点,适用范围也各不相同。蓄热材料回收法简单易实现,适用于总热量少,需要方便移动的情况;转化为其他能量的方法适用于余热量大且连续供应的情况,通常转化设备复杂;换热回收法原理简单,易于实现,通过换热器,将余热转移给需要加热的其他介质。
大尺寸常规高超声速风洞中剩余热量的特点是总量大,持续时间短,不连续供应。结合余热回收方法适用范围的分析可知,适合大尺寸常规高超声速风洞中余热回收的方法是换热回收法, 即余热回收通过将剩余热能转移给风洞来流实现。
3.2 大尺寸常规高超声速风洞的节能气动布局
经过多年的研究和发展,现有常规高超声速风洞的气动布局均能保证风洞流场具备优良的流场品质。大尺寸常规高超声速风洞的气动布局设计既要满足模拟范围,保证流场品质优良,又要满足节能,这就需要从技术成熟的常规高超声速风洞的气动布局中选择出能与余热回收技术相结合的气动布局,并将余热回收技术应用于选择出的气动布局中。
根据本文第2节中关于现有常规高超声速风洞的气动布局特点的分析可知,引射&真空-暂冲式常规高超声速风洞气动布局既具有较宽的马赫数和雷诺数模拟范围,而且在参数模拟范围内流场品质优良,又易于结合换热回收技术。将两者结合得到的适合于大尺度常规高超声速风洞的气动布局如图 7所示。
3.3 大尺寸常规高超声速风洞的节能气动布局的可行性
这种布局形式是在暂冲式常规高超声速风洞的引射-真空布局形式的基础上,通过结合余热回收技术得到新的布局形式,其主要特点表现在结构形式和运行方式上的改变。结构形式上的主要改变包括:第一,在引射分支和真空分支前,超声速扩散段后增设换热器;第二,气源出来的气体不是直接进入加热系统,而是先经过换热器,再进入加热系统;第三,去掉了真空分支的冷却器。
这种布局形式的运行方式是:从气源出来的气流经过换热器初步加热,再输送到加热器进一步加热,达到相应马赫数所需的温度,然后经稳定段、喷管,在试验段形成流场;试验后的气流经超声速扩散段减速增压,在换热器中对冷气流加热,然后进入引射分支或真空分支,排入大气。
实现这种节能布局的关键技术是高效换热器的设计。在这种换热器中,加热气流为高温低压气流;被加热气流为高压气流,其流量与加热气流的相同;换热过程要求快速且充分。如何设计出适合这种节能布局的高效换热器,需要解决以下问题,一是换热器的机理如何确定,二是换热器的性能参数如何计算,三是换热器的结构形式如何确定,等等。
普通换热器设计时,需要将冷、热介质的传输管道交叉,利用管壁的热传导换热[12]。如果风洞节能布局中的换热器采用普通换热器设计方案,则设计时需要将风洞的超扩段从风洞的高压进气管道中穿过。由于超扩段内的加热气流为高温低压气流,进气管中的被加热气流为高压气流,而且两者流量相同,因此,超扩段的直径远大于进气管道直径,而进气管道内的气流压力远大于超扩段内的气流压力。采用交叉结构形式的换热器的缺点是结构庞大、热损失大、传热速度慢以及换热效率低。
为解决上述问题,需要采用换热方式不同于普通换热器的新型换热器。一种可行的方案是换热器采用“架桥”的结构形式。在此方案中,输送冷、热气体的管道不需要直接交叉,依靠壁面传导热量,而需要在冷、热气体间设置热管作为热量传输的桥梁。用热管传热的换热器的原理如图 8所示。
由于热管传热速度快,传热效率高,只传输冷热气体间的热量,因此,相对于普通换热器,用热管传热的换热器结构简单、体积较小、热损失小且传热效率高。
目前,适用于常规高超声速风洞所需温度、压力范围内的热管,技术已经成熟,可选择的种类很多,价格也比较便宜[13]。采用热管传热的换热器的设计和制造已经可行,但尚需在实际应用中不断地优化其结构和性能。
4 新方案的节能分析
通过第2节中对于高超声速风洞工作阶段能量运行的分析,得知风洞工作时存在热能的浪费,因此,在保留暂冲-引射方案流场品质高特点的基础上,增加余热回收技术得到了新的风洞方案。实际上,高超声速风洞的运行过程不仅包括工作阶段,还包括起动阶段和结束阶段。在起动阶段,主要进行温度调节和压力调节,使来流满足风洞工作状态的总温和总压要求。风洞工作完成后,不需要来流保持工作时的状态,主要阀门开始关闭,风洞运行进入结束阶段,直到阀门完全关闭,该阶段完成。高超声速风洞运行的起动阶段和结束阶段均需要消耗大量的热能,新布局方案的节能分析需分段进行。
在风洞工作阶段,如2.1节所述,考虑到气流的沿程热损失,风洞工作阶段剩余热量估计为总加热量的80%;考虑到热管传热的换热器效率比较高,应该具有不低于80%的换热效率。因此,新布局方案在风洞工作阶段可节省的热量不低于加入热能的64%。
在起动阶段,由于气流的总温和总压不满足试验要求,在已有的方案中,这些气流的热量通常被损耗掉。风洞的起动阶段时间越长,损耗的热量越多。时间长短主要与马赫数、总温、总压调节系统和调节方法等因素有关,例如,对于采用蓄热式加热器和冷热气流掺混调节总温的风洞,起动阶段的时间约为60~100s,通常,马赫数低时时间短,马赫数高时时间长;对于采用直接加热的风洞,起动阶段的时间约为600~900s。当常规高超声速风洞采用新布局方案时,由于采用了余热回收技术,再考虑到喷管在风洞起动阶段的沿程损失小于工作阶段的损失,节省的热能不低于加入热能的70%。
结束阶段的热能损耗取决于风洞关闭系统的速率。在已有的方案中,这些气流的热量被损耗掉;在新方案中,由于余热回收技术的局限性,这些气流的热量也无法回收。另外,风洞试验全部结束后,加热器的余热在新方案和已有方案中均没有回收。相应的回收技术如何与风洞方案结合还需进一步的研究。
5 结论
在总结现有常规高超声速风洞气动布局的基础上,结合大尺寸常规高超声速风洞能量运行的特点,给出了一种新的大尺度常规高超声速风洞气动布局形式,该布局形式是节能的。同时,对于实现这种布局形式的关键技术--换热器,也给出了一种可行的方案。
鉴于本研究尚属常规高超声速风洞节能布局的初步研究,对于该气动布局更加详细的问题,如结构形式及参数、运行参数及控制等,均需要在后续工作中进一步研究。'
-
表 1 不同加热温度下实验测量值
Table 1 Experimental measurements at different heating temperatures
工况 电压/V 电流/A 加热器温度/K 气体温度/K 外壁/K 多孔电极测点温度/K TheatL TheatH Tgasin Tgasout Tsurf 测点7 测点17 测点23 测点37 测点45 测点52 1 40 0.46 363.5 372.1 293.5 295.8 294.3 335.4 339.4 343.8 350.8 353.8 354.7 2 80 0.92 578.4 612.4 295.7 312.6 297.3 479.1 504.4 516.4 551.0 560.3 574.8 3 120 1.34 810.8 861.2 298.9 345.7 297.3 670.3 738.8 759.0 814.4 828.6 834.3 4 160 1.78 877.7 932.4 300.9 360.4 305.3 706.7 808.1 845.0 887.8 890.8 906.1 注:TheatL为近气体入口端加热器温度, TheatH为近气体出口端加热器温度 表 2 不同加热温度下各比例因子对应的标准差
Table 2 Standard deviation corresponding to each scale factor at different heating temperatures
T/K 比例因子t 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 372.1 2.33031 2.32619 2.32447 2.32399 2.32667 2.33107 2.33726 2.34496 2.35466 612.4 6.75532 6.69697 6.65073 6.61661 6.59789 6.59404 6.59349 6.60450 6.63037 861.2 6.94167 6.32564 5.80576 5.40128 5.09935 4.94486 4.93141 5.05898 5.30833 932.4 8.30279 7.39442 6.54582 5.76892 5.12351 4.57371 4.20319 4.04781 4.10757 表 3 不同孔隙率下实验测量值
Table 3 Experimental measurements at different porosity
工况 孔隙率εp 加热器温度/K 气体温度/K 外壁/K 多孔电极测点温度/K TheatL TheatH Tgasin Tgasout Tsurf 测点7 测点17 测点23 测点37 测点45 测点52 1 0.2349 602.1 635.3 295.7 322.2 306.4 445.5 505.6 532.6 548.1 557.0 565.3 2 0.3471 578.4 612.4 295.7 312.6 297.3 479.1 504.4 516.4 551.0 560.3 574.8 3 0.4178 611.9 642.2 315.5 345.6 329.7 511.3 566.0 590.5 603.1 604.5 616.6 注:TheatL为近气体入口端加热器温度, TheatH为近气体出口端加热器温度 -
[1] Gupta N, Yadav G D. Solid oxide fuel cell: a review[J]. International Research Journal of Engineering and Technology, 2016, 3(6): 1006-1011. http://d.old.wanfangdata.com.cn/Periodical/xyjsclygc200508001
[2] Koteswararao P, Suresh M B, Wanic B N, et al. Review on ceramics for solid oxide fuel cells[J]. International Journal of Scientific Research in Science, Engineering and Technology, 2017, 3(8): 342-346.
[3] Zeng S M, Xu M, Parbey J, et al. Thermal stress analysis of a planar anode-supported solid oxide fuel cell: Effects of anode porosity[J]. International Journal of Hydrogen Energy, 2017, 42(31): 20239-20248. DOI: 10.1016/j.ijhydene.2017.05.189
[4] Barelli L, Bidini G, Ottaviano A. Solid oxide fuel cell modeling: Electrochemical performance and thermal management during load following operation[J]. Energy, 2016, 115: 107-119. DOI: 10.1016/j.energy.2016.08.107
[5] Boaro M, Aricò A S. Advances in medium and high temperature solid oxide fuel cell technology[M]. Cham, Switzerland: Springer, 2017.
[6] Rao Z H, Wang Q C, Huang C L. Investigation of the thermal performance of phase change material/mini-channel coupled battery thermal management system[J]. Applied Energy, 2016, 164: 659-669. DOI: 10.1016/j.apenergy.2015.12.021
[7] 姚凯, 郑会保, 刘运传, 等.导热系数测试方法概述[J].理化检验(物理分册), 2018, 54(10): 741-747. http://d.old.wanfangdata.com.cn/Periodical/lhjy-wl201810007 Yao K, Zheng H B, Liu Y C, et al. Survey of measurement methods for thermal conductivity[J]. Physical Testing and Chemical Analysis (Part A: Physical Testing), 2018, 54(10): 741-747. http://d.old.wanfangdata.com.cn/Periodical/lhjy-wl201810007
[8] 刘世杰, 吴鹏章, 王梦蛟, 等.一种基于稳态热流法的导热系数测定仪器及方法[J].橡塑技术与装备, 2017, 43(17): 45-47. http://d.old.wanfangdata.com.cn/Periodical/xsjsyzb201717010 Liu S J, Wu P Z, Wang M J, et al. An instrument and method for measuring the thermal conductivity based on steady-state heat flow method[J]. China Rubber/Plastics Technology and Equipment, 2017, 43(17): 45-47. http://d.old.wanfangdata.com.cn/Periodical/xsjsyzb201717010
[9] 任佳, 蔡静.导热系数测量方法及应用综述[J].计测技术, 2018, 38(S1): 46-49. http://d.old.wanfangdata.com.cn/Periodical/hkjcjs2018z1014 Ren J, Cai J. Summary of measurement methods and applications of thermal conductivity[J]. Metrology & Measure-ment Technology, 2018, 38(S1): 46-49. http://d.old.wanfangdata.com.cn/Periodical/hkjcjs2018z1014
[10] Radovic M, Lara-Curzio E, Trejo R M, et al. Thermophysical properties of YSZ and Ni-YSZ as a function of temperature and porosity[J]. Advances in Solid Oxide Fuel Cells Ⅱ: Ceramic Engineering and Science Proceedings, 2009, 27(4): 79-85. http://cn.bing.com/academic/profile?id=8bebe7971bd1bf149388c9bc1e7ce6f1&encoded=0&v=paper_preview&mkt=zh-cn
[11] 付文强, 高辉, 薛征欣, 等.多孔材料有效导热系数的实验和模型研究[J].中国测试, 2016, 42(5): 124-130. http://d.old.wanfangdata.com.cn/Periodical/zgcsjs201605026 Fu W Q, Gao H, Xue Z X, et al. Experimental measurement and calculation of thermal conductivity of porous material[J]. China Measurement & Test, 2016, 42(5): 124-130. http://d.old.wanfangdata.com.cn/Periodical/zgcsjs201605026
[12] 王刚, 魏高升, 黄平瑞, 等.改进的新有效介质理论模型分析多孔绝热材料的有效导热系数[J].中国电机工程学报, 2016, 36(9): 2465-2469. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdjgcxb201609019 Wang G, Wei G S, Huang P R, et al. Effective thermal conductivity analysis on porous thermal insulation material by the improved novel effective medium theory model[J]. Proceedings of the CSEE, 2016, 36(9): 2465-2469. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdjgcxb201609019
[13] 付俊鹏, 蔡九菊.基于谢尔宾斯基地毯模型对烧结矿散料有效导热系数的研究[J].冶金能源, 2017, 36: 59-61. http://www.cqvip.com/QK/95660X/2017A01/673049683.html Fu J P, Cai J J. Research of the effective thermal conductivity of sinter packed based on sierpinski carpet[J]. Energy for Metallurgical Industry, 2017, 36: 59-61. http://www.cqvip.com/QK/95660X/2017A01/673049683.html
[14] 王世芳, 吴涛.多孔介质有效热导率的一种新模型[J].工程热物理学报, 2016, 37(12): 2626-2630. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb201612022 Wang S F, Wu T. A new fractal model for the effective thermal conductivity of porous media[J]. Journal of Engineering Thermophysics, 2016, 37(12): 2626-2630. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb201612022
[15] Zhai S P, Zhang P, Shi B, et al. Effective thermal conductivity of polymer composites: Theoretical models and simulation models[J]. International Journal of Heat and Mass Transfer, 2018, 117: 358-374. DOI: 10.1016/j.ijheatmasstransfer.2017.09.067
[16] Carson J K, Lovatt S J, Tanner D J, et al. Predicting the effective thermal conductivity of unfrozen, porous foods[J]. Journal of Food Engineering, 2006, 75(3): 297-307. DOI: 10.1016/j.jfoodeng.2005.04.021
-
期刊类型引用(2)
1. 时文,乐嘉陵,田野. 污染组分对超燃冲压发动机工作特性影响. 航空学报. 2024(19): 150-166 .  百度学术
百度学术
2. 朱涛,杨凯,朱新新,徐洋,王辉. Schmidt–Boelter热流传感器的改进和性能测评. 实验流体力学. 2024(06): 99-105 .  本站查看
本站查看
其他类型引用(1)







 下载:
下载: