The statistics of velocity and temperature fluctuations in axisymmetric laminar-to-turbulent transitions
-
摘要: 热力学平衡系统连续相变的理论方法,被推广用来讨论圆管内轴对称层流到湍流转捩区间的流动和振荡特性。假设在转捩区间径向脉动速度与充分发展区的湍流在数值上完全相同,在每一个截面上转捩流动可以看成是充分发展区的层流和湍流的合成流动。湍流成分的合成比例作为序参数用来定义合成流动。引入合成比例的振荡后,运用最小熵产生准则得到一个可以描述转捩行为的方程。采用相同的处理方法讨论了加热圆管内转捩区间的对流传热特性。在圆管内的流动和对流传热允许相似和独立的转捩过程,在转捩区间宏观振荡同时具有随机性和确定性。最后与实验进行了对比,包括流动和传热实验得到的测量结果。Abstract: The procedures for studying continuous phase transitions of thermodynamic equilibrium systems are extended to discuss the laminar-to-turbulent transitional flows in circular tubes. The flow in the transition range is treated as a composition of the laminar and turbulent flows assuming that the radial fluctuating velocity has the same value as that of the fully turbulent flow. The composite ratio of the turbulent flow is used as an order parameter to define the composite flow. The fluctuations of the composite ratios are introduced, and the criterion of minimum entropy production is used to derive an equation which can describe the transition behaviors. The convective heat transfer characteristics in the transition range in a heated circular tube are also discussed adopting the same procedures. Similar and separate processes for the transitions of the flow and convective heat transfer types are allowed in the heated circular tube. The macroscopic fluctuations in the transition range show both probabilistic and deterministic characteristics simultaneously. The agreements with measurements are given including those obtained in flow and heat transfer experiments.
-
Keywords:
- transition range /
- composite flow /
- fluctuations /
- minimum entropy production
-
0 引言
由于流体流动状态对实际应用的重要性,人们对流体从层流到湍流的转捩流动进行了大量研究。对于圆管内的流动,自1883年雷诺最初的实验起,就已知当雷诺数Re(Re=ρUd/μ,是一个由密度ρ、平均流速U、管径d和粘性系数μ组成的无量纲参数)约为2300时开始自然转捩。实验结果显示,存在转捩起始雷诺数(记为ReL)和转捩终止雷诺数(记为ReR)。由此可以定义转捩区间,即从ReL到ReR的流动雷诺诺数区间。转捩在哪个雷诺数起始是一个与具体情形有关的问题,与管内的扰动相关,强迫转捩具有非常不同的起始雷诺数[1-2]。
在转捩区间流体的流动会出现两种典型的瞬时不规则流动,称为Puff和Slug,它们均与常规的湍流不同[1, 3]。这是间歇性理论不能解释的。在转捩区间流体轴向速度的振荡,具有确定的且仅与Re有关的统计特性[2]。流动振荡的统计特性在转捩区间内如何演化发展,缺乏理解。从1883年至今已过去了130多年,对于层流到湍流的转捩过程仍然没有广为接受的理论进行解释。
流体力学方程也称为N-S方程,用来描述流体的流动。实验结果说明,圆管内的Hagen-Poiseuille流动是线性稳定的,即使在Re很大时也需要有限幅度的扰动才能激发转捩[3-4]。在一定的流量或Re条件下,许多证据均使人产生这种看法,即圆管内流动的非线性流体力学方程至少有两类解,一类是层流解,另一类是物理量有明显脉动的湍流解。如果视转捩区间的流动为第三类解,那么可以认为圆管内流动的流体力学方程有三类解。转捩为什么开始,随着Re增加如何演化发展,加上流体力学方程解的唯一性问题,对流体力学提出了巨大挑战。圆管内转捩流动的本质仍是流体力学的一个未解之谜,转捩区间的对流传热特性也是如此。
有的层流到湍流的转捩很早就被视作是非平衡热力学系统的相变[5]。序参数通常与系统的结构或对称性相关,用于描述平衡系统的相变(如正常导体到超导体的变化)。Landau和Lifshitz在给出热力学平衡系统第二类相变的处理方法时,讨论了序参数的振荡[6]。靠近相变点时,存在一个很窄的温度区间,其中热力学函数的物理本质取决于序参数振荡的反常增加。这个区间称为振荡区间,序参数的振荡占据主导地位。在圆管内层流到湍流的转捩过程中,已经测量到很大的振荡[2, 7-8]。层流到湍流的转捩和平衡系统的连续相变之间,已发现惊人的相似性。尽管文献[9]指出,许多关于平衡相变的认识可以推广应用到非平衡情形,但采用非平衡相变观点来对流动转捩进行的讨论仍然很少。
在本文中,关于热力学平衡系统连续相变的理论方法,被推广用来讨论层流到湍流转捩区间的轴对称流动特性。讨论共分3个步骤。第一步,给出层流到湍流的转捩和平衡系统的连续相变之间的相似性,并给出关于后者采用序参数的通用热力学理论方法。第二步,在每一个截面上转捩流动被分解成充分发展区的层流和湍流成分,采用的假设是在转捩区间和充分发展区的湍流中径向脉动速度在数值上完全相同。湍流成分的合成比例作为序参数用来定义合成流动。引入合成比例的振荡后,运用最小熵产生准则[5]得到一个可以描述转捩行为的方程。论述了对于转捩流动的理解方法,指出了本文推导方法与平衡相变热力学理论的相同之处。采用相同的处理方法讨论了加热圆管内对流传热特性的转捩行为。在最后一步,与实验进行了对比,包括流动和传热实验得到的结果。
1 层流到湍流的转捩和连续相变之间的相似性
在自然界中相变很常见,常发生在磁体、液晶、超导体、晶体和液体凝固中。在平衡系统内,通过改变热力学变量,如温度、压强或磁场强度,系统的性质会发生显著的变化,此时系统状态会发生转变,进入明显不同的状态,这称为相变[10]。
平衡相变可以分为两类,即不连续相变和连续相变。不连续相变也称为一级相变,相变时有潜热发生,熵的变化是不连续的。除一级相变外的所有其他相变统属于二级相变或连续相变,相变时无潜热发生,熵的变化是连续的[10]。对于连续相变,自由能的一阶到n-1阶导数连续,但是第n阶导数不连续(n大于等于2)。Landau和Lifshitz称连续相变为第二类相变[6]。
层流到湍流的转捩和平衡系统的连续相变之间,已发现显著的相似性。首先,存在一个转变发生时的临界点。对于平衡系统的连续相变来说,在低于临界点时一个相存在,在高于临界点时另外一个相存在。两个相具有明显不同的行为,分别与其结构或对称性一致。湍流和层流在很多方面显著不同,包括流动的形貌、流动变量的剖面或分布、摩擦因子和热流等。在和相变的定义对比之后,可以理解流动转捩现象被当成非平衡相变的原因。
其次,靠近相变点时,存在一个很窄的控制参数区间,其中序参数会出现很大的振荡,并支配着系统的性质[5]。流动的转捩区间看上去并不窄,似乎与平衡相变的窄的振荡区间不同。在平板表面上受控的流动转捩,可以在空间上有很长的转捩距离。另外,轴对称流动的Re可以很容易地处在转捩区间内。对于轴对称流动,ReL和ReR的差别实际上很小,这可以从Durst和Ünsal在很大Re范围内进行的测量数据中看出[2]。对于平衡系统的连续相变来说,在接近临界点时,系统会在微观上进行“调整”,表现出物理量大的振荡和长程有序,似乎在“预示”着将进入新的状态[5]。在圆管内的转捩区间已经测得速度有很大的振荡,比湍流的还大5倍。Durst和Ünsal称速度这种反常的大的振荡为过冲(Overshoot)[2]。在转捩区间,流动里包含长程相关(Long Range Correlation)的相干结构, 表现出集体运动特性。
第三,在相变点附近大的振荡,同时表现出随机性和确定性特点。对于平衡系统的连续相变来说,在临界点邻域里系统的行为和微观细节关系不大,貌似迥异的系统具有很多相同的性质,包括物理量大的振荡特性[10]。这被称为平衡相变的临界普遍性现象。尽管层流到湍流转捩的临界现象缺乏深入的理解,但是实验证据表明转捩行为与扰动的产生方法无关。流动扰动的不同产生方法,初始扰动的不同幅度,不同的起始雷诺数ReL,导致的转捩均具有相似的过程,大的随机振荡具有相同的仅依赖于Re的统计特性[2-3]。
除了上述相似性外,层流到湍流的转捩和平衡系统的连续相变,二者对研究带来了两个相似的困难或挑战。首先,二者均给物理学带来(或曾经带来)巨大的挑战。对于平衡系统来说,配分函数是否包含对相变的描述,曾经是物理学家的重大忧虑。配分函数只是解析因子的求和,但是系统可以表现出相变这样的奇异行为。对于圆管内层流到湍流的转捩,有的研究者怀疑N-S方程的适用性,有的则怀疑N-S方程是否允许多个解。其次,难以确定相变或转捩的本质,或者说难以解释其为什么开始。对于平衡系统的连续相变,微观相互作用无疑是产生相变的根源,但是相变的本质却难以理解,相变的预测也极其困难[10]。这些与圆管内层流到湍流的转捩十分相似。即使已知流动转捩会发生,也难以预测准确的转变点。
上述相似性导致了把圆管内层流到湍流的转捩过程当成非平衡相变。许多关于平衡相变的认识可以推广应用到非平衡情形[9]。这很自然地使人采用平衡系统连续相变的观点,来理解层流到湍流的转捩流动。为此,在下一节简要给出处理平衡系统连续相变的通用热力学理论方法。
2 连续相变的Landau理论
在连续相变中,一相的结构通常具有较低的对称性。例如,在顺磁系统向铁磁系统的相变中,自发磁化出现,从而在空间选出了一个确定的方向,转动对称性被打破。在超导相变中被打破的是规范对称性。在相变时一部分电子能够形成“束缚对”,这些“束缚对”形成一个宏观占据的量子态,相干地作用着,形成凝聚相。当外加一电场时,这个凝聚相作为整体运动,不因摩擦而显著减速[5, 10]。
统计物理认为一个平衡系统的所有统计信息,都包含在配分函数Z内:

(1) 其中,N是系统内的粒子数,V是其体积,T是其温度,E是其能量,kB是Boltzmann常数,i表示系统所有可能的微观状态。系统的Helmholtz自由能或简称自由能为:

(2) 自由能F是一种热力学势[5-6, 10]。如果自由能已知,所有可观测量均可通过F的合适导数得到。
在相变点系统经历的是定性行为的变化,并发展出某种前所未有的有序。因此系统作为可观测量的函数,其变化是不连续的。如果这个可观测量是温度T,就意味着自由能F(T)在相变点是非解析函数。这是相变理论的出发点。非解析函数在某些点或奇点,它的一些导数没有定义。相变点对应于这些自由能奇点的点或点集(在温度、压强、磁场等变量的参数空间)。在经过相变点时自由能是不连续的从而系统的行为也是不连续的。
在(1)式中,求和的每一个指数项在温度有限时均是解析的,配分函数是这些指数项的求和,因此直观上难以理解配分函数会有非解析行为。自由能F的奇点的存在性,已被证明是热力学极限(N→∞, V→∞,而N/V保持不变)的直接结果。也就是说,配分函数的奇异性是热力学系统本质上无穷多自由度的结果[5, 10-11]。
20世纪30年代,Ginzburg和Landau提出了一个连续相变的理论,把序参数和系统的结构或对称性联系起来[5]。对于从无序相到有序相的连续相变,在临界点普遍特点是在有序相(具有更少对称性)内部出现某种新的宏观参数。这个特殊的参数常常和在临界点被打破的对称性相关,是系统出现的有序的一种度量,在Ginzburg-Landau理论中称为序参数[10]。这个理论通常也称为Landau理论,认为系统用一个宏观态就足以描述。
在Landau理论中,系统的自由能以这种方式近似:既能够表现出相变的非解析性,又能够反映大部分物理。其处理方法主要包含以下4步:
(1) 定义序参数η。对确定系统必须定义序参数,它在无序相为0,在有序相不为0。
(2) 假定自由能函数形式:

(3) 其中F0是温度的解析函数,FS(T, η)包含了所有依赖于η的信息。自由能通过上述函数对η求极小值来确定。系统的非解析行为包含在上述函数的求极小值过程中[5]。
(3) 构建FS(T, η)。假定FS(T, η)是η的解析函数(以多项式展开为典型),遵从所有与η有关的对称性。这一步是Landau理论中最重要部分,其中包含了系统的大部分物理。
(4) 温度相关性。假定所有与温度相关的重要特性,都包含在FS(T, η)展开式的最低阶项中。记Tc为相变的临界温度,FS(T, η)的展开式具有如下典型的形式[5]:

(4) 由于FS(T, η)被构建为展开式,因此有像α2和α4这样的未知参数。对一个物理系统,这些参数依赖于温度。如果它们和温度的关系是连续的,那么在相变点附近可以忽略这些依赖关系。对于连续相变来说,这是严格成立的。
通过构建FS(T, η)并对η求极小值,得到系统的自由能,η作为温度的函数得以确定,相变的本质就确定了。这意味着η的平衡值满足:

(5) 这里可以看出Landau理论的精神,该精神清楚地表述在文献[6]中。在对待序参数的处理方法中,η不是先作为温度(和其他变量)的确定函数,而是先作为独立变量,然后其平均值通过对自由能或热力学势求极小值来确定。在Landau理论中系统采用均匀或平均状态来表征,因此它是一个平均场理论,在其处理方法中忽略了相变点附近序参数的振荡。
对于平衡系统,粒子间的微观相互作用是产生相变的根本原因[10]。在相变点附近,粒子间的微观相互作用给自由能带来了额外项,它们与系统在相变前后不同的结构或对称性相关。尽管平衡相变的临界普遍性现象在很大程度上得以解释,对许多情形只能近似确定相变点,原因是不清楚如何精确定量地描述这些微观相互作用。
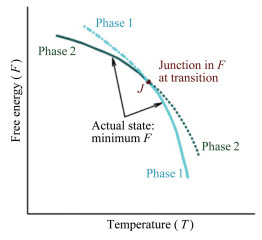
Landau理论把额外的自由能当成温度和包括η在内的其他变量的解析函数[10]。这些与系统结构或对称性相关的额外项是序参数的非线性函数,在有的情形其形式如(4)式。这种非线性为系统的多种行为提供了可能性,可以从图 1看出。
图 1示意了在相变点附近两相自由能的变化。实线表示现实中存在的两相,虚线表示假想没有发生相变时的两相。可以看出系统有两个相,F取极小值要求在交点J处发生相变。离开J点,两相具有不同的结构或对称性,采用序参数η表示。最小自由能原理确定现实中哪一相存在。
从图 1可以看出,真实的相变点是系统热力学函数的奇点。对于连续相变,相变点J等价于振荡区间,其中系统的物理本质由序参数振荡的反常增加而决定。这种振荡的增加,是由相变点附近最小自由能的扁平化造成的。在相变点附近,对应于不同η的自由能其差别如此之小,导致在付出自由能代价很小的情况下,系统的序参数也可以在很大的范围内自如地振荡。也可以说,热力学势对应的恢复力如此之小,以致于系统要花很长时间才能稳定在η平均值对应的状态。即使很轻微的扰动,对η平均值的影响也很大,系统内η存在很大的随机偏离[6]。
在当代Landau理论是一个通用的相变理论[10]。作为一个平均场理论,它在振荡区间失效。但是它得到的如(3)式那样的近似自由能,是考察振荡效应的自然出发点。在文献[6]中采用这种近似的自由能讨论了序参数的振荡。在给定温度(和其他除了η外的变量)下,使系统离开平均状态所需要的最小功,等于η的变化引起的热力学势的变化δF。在这些条件下,振荡几率w为:

(6) 下面记η的平均值为η。对相对于η的小的偏离,有:

(7) 振荡几率w为:

(8) 因此振荡的方均根值为:

(9) 可以用感受率χ来代替上式中的导数:

(10) 感受率χ的定义在文献[6]中给出,(4)式成立时其表达式为:

(11) 当T→Tc时χ趋向于无穷,是临近相变点时自由能极小值作为η的函数扁平化的自然结果。同样,当T→Tc时η的振荡也会反常增加。文献[6]进一步论述,在临近相变点时,反常增加的是长波振荡,振荡的相关半径(Correlation Radius)以

3 采用非平衡相变观点对轴对称层流到湍流转捩的理解
为了简洁,本节仅考虑没有传热发生的流动。如果没有传热,很容易在圆管内产生没有进口效应且看上去间歇的轴对称流动,其雷诺数处于转捩区间。这样,可以很方便地研究确定雷诺数下的轴对称转捩流动。
非线性流体力学方程能够准确描述流体的流动。对于层流、转捩和湍流流动,可以把下面的三维非定常N-S方程组作为研究出发点[12]:

(12) 
(13) 其中t为时间,ρ为微元体δV内流体的密度,v为其速度矢量,p为其压强,



(14) 这里主要对图 2所示的圆管内的流动感兴趣。如果管子的长径比很大(如大于500),就可以研究进口效应可忽略的充分发展区的定常流动。在图 2中,离入口更远的颜色较深区域里的流动属于充分发展区的定常流动。对于圆管内充分发展区的定常层流和湍流,流体力学方程可以简化[12-13],分别写成下述2个方程:

(15) 
(16) 在(15)和(16)式中,采用了图 2所示的轴对称坐标系,u是流体微元沿x方向的速度(轴向速度),v是流体微元沿r方向的速度(径向速度)。对于湍流变量,物理量上方有“-”的表示时间平均值,物理量上方有“~”的表示瞬时值减去平均值,称为脉动值。在(15)式中,层流物理量用变量上方没有“-”或“~”来表示。流动是定常和轴对称的,p=p(x),u=u(r),p=p(x),u=u(r),v=0,ũṽ只和r有关。可以看出,所研究的流动系统是垂直于x方向的一个平面内的所有流体微元,并且感兴趣的是时间平均行为。
由于感兴趣的是时间平均行为,对于Re处于转捩区间的充分发展区的转捩流动,求解方程的形式应当与(16)式相同。当然需要采用不同的符号来表示变量。实际层流内包含小扰动,也可以用ũṽ项来描述。对于层流来说此项很小而常常忽略。比较求解速度的方程,对于层流来说是(15)式,对于湍流(和转捩流动)来说是(16)式,可以看出,如果认为层流的ũṽ项为0,那么不同类型的流动遵从相同的通用方程。该通用方程在形式上与(16)式相同。
在流体力学方程中,(13)式包含非线性项▽·(ρvv),该项导致(16)式内有

在每个流体微元内部有大量的分子,一直在相互碰撞。这些碰撞不会使系统的能量和动量产生或消失,但是由于流体微元内机械运动速度的不均匀分布,它们会产生熵增。因此每个流体微元是非平衡的,内部有把可用能转化为无用热能的熵产生过程。为了维持稳定存在,非平衡系统往往是开放系统[5],物质、动量和/或能量必须从其边界流进流出。对于所研究的系统(垂直于x方向的一个平面内的所有流体微元),这些自边界流进流出的流,与


流体力学系统的熵平衡方程在文献[5]和[16]中给出。对于无传热发生的流动,熵平衡方程为:

(17) 其中,s表示流体微元的熵,上标S表示对称,(▽v)S是对应于张量▽v的迹为0的对称张量,算子:表示张量的缩并。在轴对称坐标系中,(▽v)S为:

(18) 其中Tr表示张量的迹,Û是单位二阶张量,vx是沿x方向的速度,vr是沿r方向的速度,上标T表示转置。(18)式同时适用于层流和湍流,此处采用vx和vr来表示流体的瞬时速度。
由于流体微元内伴随分子碰撞的耗散过程,熵平衡方程具有源项,采用(17)式的右端项来描述。这些耗散过程改变着机械运动速度的非平衡(非均匀)分布,驱使流体微元趋向平衡,并产生熵增。(17)式右端的整个源项称为熵产生σ,在轴对称坐标系中为:

(19) 对于圆管内充分发展区的层流,

(20) 对于圆管内充分发展区的湍流,

(21) 在上两式中,下标Lam表示层流,下标Turb表示湍流。
熵平衡方程可以由(12)和(13)式以及能量守恒方程推导得到[5, 12, 16]。在推导过程中,利用了一些热力学平衡关系式,如状态方程,这在局部平衡假设(机械运动速度的非均匀分布对热力学关系式影响不大)下成立。由于可以从其他流体力学方程导出,熵平衡方程并不给出关于非平衡系统的额外信息,在很多的实际求解过程中没有显式地利用它。这与平衡系统的情况是一致的。对于平衡系统,热力学第二定律很少显现在实际求解应用中(除了出现多解的情形,如去除膨胀激波解)。最小自由能原理可以从热力学第二定律导出,如果没有相变发生(系统处于已知的相态),也很少显现在实际求解应用中。它们在那些求解过程中是自动满足的。
对于非平衡系统,Ilia Prigogine提出了最小熵产生的稳定性准则。该准则断言,对于非平衡系统来说最小熵产生对应的状态是一个定态[5, 17-18]。在广义流(如应力张量

对于所考虑的流体力学方程,

非平衡系统的稳定性取决于一些参数或参数的组合[5, 18]。当这些参数或组合靠近临界点时,流体力学方程的非线性使系统变得不稳定,此时就会发生非平衡相变。每个稳定的非平衡相要求这些参数或组合满足一定的条件。在两个不同的相之间,有一个转捩区间,其中有很大的振荡发生。正如McComb所述[7],在圆管流动实验中,当流速达到一定数值时,会达到临界Re,压力计的读数开始剧烈震荡。这种现象在一个速度区间内一直持续,直到流速达到某个数值,压力计读数恢复平稳,随后压力计读数保持平稳。McComb称此为“奇怪效应”。
层流流动中的扰动表现为速度的脉动,尽管流动转捩需要它们,但是转捩行为与扰动产生的方法无关。采用不同方式来产生流动扰动,初始扰动的幅度不同,转捩的起始Re不同,导致的转捩均具有相似的过程,大的振荡具有相同的依赖于Re的统计特性[2-3]。
湍流流动包含有相干结构,使得其与层流流动显著不同。在非平衡相变中常常观察到具有对称特点的结构形态。相变时,系统在时间和/或空间上的对称性被打破,新的非平衡态展现出比初始态更多的结构。这些新的动力学形态被Prigogine称为“耗散结构”(Dissipative Structures)[19]。由于对非平衡热力学的贡献,尤其是耗散结构理论,Prigogine在1977年被授予Nobel化学奖。
从上述论述可以看出,层流到湍流的转捩过程,可以理解为非平衡相变。理解要点如下:
(1) 层流和湍流流动是圆管内轴对称流动的两个非平衡相,两相之间会发生转捩。转捩受流动参数(参数组合为Re)控制,并需要层流流动中表现为速度脉动的扰动。
(2) 当Re靠近临界点时,流体力学方程中的非线性使流动变得不稳定,此时会开始非平衡相变即转捩。转捩时,流动变量会出现大的振荡,预示着流动将进入新的状态。流动系统中的宏观振荡同时表现出随机性和确定性的特点。
(3) 在转捩后,新的稳定非平衡态为湍流流动,其内包含特有的结构形态。湍流内新的结构形态类同于耗散结构。
(4) 难以准确预测转捩点,湍流内新的结构形态的细节也难以准确描述。
上述要点与平衡系统连续相变的特点是一致的。仿照第2节给出的Landau理论的步骤,最小熵产生的稳定性准则可以用来处理圆管内的流动转捩。为了应用此准则,首先要找到表征转捩的序参数和熵产生。由于转捩点难以准确预测,对转捩区间内宏观振荡的理解应当成为研究重点。
4 圆管内层流到湍流转捩中的振荡
4.1 合成流动观点
首先考虑无传热发生时圆管内的转捩流动。对于时间平均行为,此处采用假设:在转捩区间内脉动速度ṽ与全湍流流动中的一样。下面将说明,在此假设下,在每一个截面上的转捩流动,可以看成是充分发展区的层流和湍流的合成流动。x方向的速度包含两个部分,即为层流部分和湍流部分。层流的合成比例用1-η表示,湍流的合成比例用η表示。在某一截面上,η相同且忽略其随x的变化。本文称此为“合成流动观点”。
对于转捩流动,在合成流动观点成立时x方向速度的变化为:

(22) 其中下标Tran表示转捩,层流和湍流的物理量的表示方法与(15)和(16)式中的一样。(16)式可以改写为:

(23) 其中忽略了实际层流中的ũṽ项。可以重新改写(23)式为:

(24) 现在可以看出,对于转捩流动,沿x方向合成的平均速度为:

(25) 沿x方向合成的脉动速度为:

(26) 沿r方向合成的平均速度为0,沿r方向合成的脉动速度为:

(27) 可以看出,(15)和(16)式允许采用合成流动观点。为了简洁,忽略了沿x方向的脉动速度,因此在(22)~(24)式中有忽略项。当然,实际层流中沿x方向的脉动速度不为0。考虑层流流动里沿x方向的脉动速度时,可以重写(26)式并代入(16)式中,然后就可以发现在(22)~(24)式中出现了一些额外项,正是那些被忽略的项。并且,可以发现考虑层流流动里沿x方向的脉动速度时,并不影响把转捩流动当成充分发展区的层流和湍流的合成流动。因此,合成流动的观点,对于转捩流动的方程来说是严格允许的,只要在转捩区间内脉动速度ṽ与全湍流流动中的一样。
在转捩区间和全湍流流动中ṽ具有一样数值的假设,可以进行进一步解释。众所周知,即使Re很高时也需要有限振幅的扰动才能引发转捩,因为圆管内的层流流动是线性稳定的[2, 4]。在圆管内流动开始转捩,其原因是Re的增加和管内有限振幅的扰动。对于管内确定的转捩流动,这个假设相当于说,无论流动状态是层流、转捩还是湍流,ṽ的数值均相同,而且这个ṽ产生于入口或管壁引入的有限幅度的扰动。流动里的扰动表现为三维脉动速度,沿周向的脉动速度不影响上述推导。为使质量守恒方程(12)在每一瞬间成立,可能需考虑沿周向的脉动速度。
4.2 序参数和它的振荡
在第3节曾提到,为了应用最小熵产生稳定性准则,首先要找到表征转捩的序参数和熵产生。对于从无序相到有序相的连续相变,在临界点的普遍特点是在有序相内部出现某种新的宏观参数。这个特殊的参数是系统出现有序的一种度量,在Landau理论中称为序参数[5, 10]。对于流动转捩,在湍流中出现的新的宏观参数包括

对于连续相变,在临近相变点时存在一个振荡区间,其中允许序参数的大幅振荡。应当引入η的振荡来描述转捩流动里的大的振荡。因此在转捩流动里,η由两部分组成,即平均值η和脉动值


(28) 其中,η取值在0到1之间,是在ReL和ReR之间的单调递增函数,

在描述转捩流动的瞬时状态时,引入η和


在每一瞬间,每一截面上只允许一个压强梯度,因此在每一截面η和



(29) 沿x方向合成的脉动速度为:

(30) 沿r方向合成的脉动速度永远是ṽ。把它们以及η和


(31) 其中,n和m都是正整数,

(31) 式的成立,其原因在于脉动或者振荡的两种产生机制。ũ的统计特性由湍流这种流动模式决定。从(9)式可以看出,对于连续相变,序参数的振荡由靠近相变点时最小自由能的扁平化引起。

4.3 平均合成熵产生
对于无传热发生的转捩流动,沿x方向合成的平均速度是(29)式,沿x方向合成的脉动速度是(30)式,沿r方向合成的脉动速度永远是ṽ。对于转捩流动,熵的平衡方程与(17)式一样,因此可以从(19)、(29)和(30)式导出熵产生。根据(19)、(29)和(30)式,对于圆管内转捩流动的一个流体微元,其平均熵产生为:

(32) 在导出(32)式时,利用了形如(31)式的一些统计无关性关系式。
(32) 式的右端项,使人想到处于平衡态的二元混合物的自由能,其相变的处理方法在文献[5]和[10]中给出。仿照二元混合物混合自由能的定义[10],对于圆管内转捩流动的一个流体微元,其平均合成熵产生定义为:

(33) 其中下标c表示合成。
根据最早由Prigogine提出的最小熵产生稳定性准则,η的取值应当使σTran, c取极小值。这要求(33)式对η的导数等于0。这与处于平衡态的二元混合物的处理方法相似[10],尽管在机械运动速度非均匀的情况下,流体微元的熵产生与二元混合物自由能之间的对应关系仍然需要进行研究。称η项为(33)式右端第一个方括号内的所有项。(33)式右端第二个方括号内的所有项随r变化而变化,但是η不随r变化。令η项对η的导数为0,即:

(34) 这个η的取值对应于在转捩区间需要维持流体微元运动的最小熵产生。由于η是Re的函数,并且



关于相变的Landau理论不考虑序参数的振荡,因此在振荡区间不适用[6, 10]。在振荡区间,热力学势不能仅仅展开成序参数(和其空间导数)和其他热力学变量的函数。这里考虑了η的振荡。推导(34)式的过程,在对待序参数的处理方式上与Landau理论的精神一致,也就是说,在通过对热力学势求极值来确定序参数时把它看成是与热力学变量地位相同的独立变量[6]。
(34) 式表明包括振荡在内的转捩行为,与层流或时间平均湍流的剖面信息无关。这与相变的临界现象一致。靠近临界点时,系统的微观性质不影响系统的热力学行为,不同的系统可以有许多相似的性质[10]。
文献[10]中给出的二元混合物相变的处理方法等价于Ising模型,其平均场处理步骤完全对应于在第2节给出的Landau理论的步骤。表 1列出了二元混合物相变和圆管内流动转捩的对比。
表 1 二元混合物相变和圆管内流动转捩的对比Table 1 Analogies between the phase transition of a binary mixture and the flow transition系统 序参数 热力学函数 处理方法 二元混合物(平衡系统) 浓度x或其线性函数 自由能,混合自由能 混合自由能取极小值来确定x(Landau理论的精神) 一个截面上的流体微元(非平衡系统) 合成比例η或其线性函数 平均熵产生,平均合成熵产生 平均合成熵产生取极小值来确定η(利用了Landau理论的精神) 4.4 无传热发生时在转捩区间的振荡
在上述推导中,不考虑传热发生,忽略了温度的变化。对于无传热发生的情形,多出了两个变量即η和

对于所研究的转捩流动,η是Re的函数。此处假定


(35) 那么


(36) 转捩开始于ReL并且结束于ReR,因此对η的约束条件为:

(37) 在层流区和湍流区η的振荡为0,并且η是Re的单调递增函数,因此对η导数的约束为:

(38) 满足所有这些条件的解为:

(39) 常数C为:

(40) 把(39)和(40)式代入(35)式得到

由此可以看出在转捩区间的宏观振荡同时表现出随机性和确定性的特点。
4.5 有对流传热发生时在转捩区间的振荡
如果图 2所示的圆管由钢制成,且在管子两端有电势差,那么电流和管壁电阻一起作用会在管壁内会产生热量。当流体(如正十烷)在管内低速流动时,会发生在恒定流量和几乎不变热流条件下的对流传热。
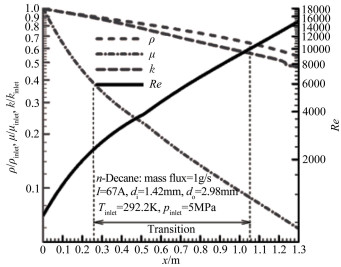
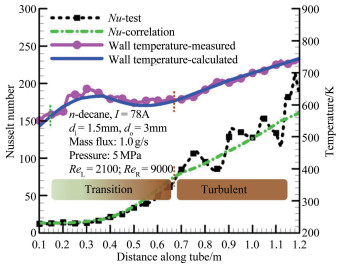
在流动时,正十烷吸收热量后温度升高,导致密度和粘性系数降低。在合适的流量、管子内径di和电流等参数条件时,正十烷在电加热圆管中会建立定常流动和对流传热,并且由图 3看出,流动的雷诺数Re可以自入口的不到1000增加至出口的超过10000。在图 3中,不同温度和压强下正十烷的密度ρ、粘性系数μ和热传导率k,采用一个碳氢化合物的物性程序计算得到。自然转捩在Re约为2300时开始,结束于另外一个Re,对于流动小于4000,对于传热小于10000[13, 20-21]。因此,这个特殊的加热流动使得可以研究在管内完整的无明显进口效应的转捩过程。
中等热流情形下流动和对流传热的转捩,在文献[22-23]中已完整给出。整个推导过程有点冗长。这里对求解速度和温度的方程间的相似性感兴趣。
对于时间平均行为,(16)式为适用于不同类型流动的求解速度的通用方程。可以写出一个适用于湍流的求解温度的方程,以此来作为另一通用方程。为了清楚对比,把它们写在一起[13]:

(41) 
(42) 在(42)式中应用了变量分离方法,即:

(43) 在(43)式中,Λ(x)没有脉动部分,描述的是壁面热流引起的平均温升,Θ(r)描述的是截面内沿r方向的温度剖面,对于湍流它包含时间平均值Θ(r)和脉动值

对比(41)和(42)式,可以发现它们在形式上是相似的。雷诺比拟原理(The Theorem of Reynolds’Analogy)指出,在湍流中导致动量和热量进行传递的机制是相同的[13]。可以断定在湍流中




由于质量守恒,无转捩发生时ρu随x的变化为0(ρ和u的积在不同截面的相同r位置上相同)。在中等热流情形下,在转捩区ρu随x的变化对(42)式性质的影响很小。根据(41)和(42)式,求解速度和温度的方程之间是弱耦合的,这种耦合是通过温度和压强影响物性而发生的。
在层流、转捩和湍流的流动和传热里变量剖面的类型分别是确定的,每一流动或传热类型均具有特有的剖面。流体的热物性如μ和k受剖面影响。但是决定剖面类型的是Re,热物性仅能在数值上影响剖面。可能有人会说控制(41)和(42)式转捩的参数不一定相同,这里遵照文献[20-21]认为控制参数均是Re。这两个相似并弱耦合的式子具有这种性质,速度剖面的类型不影响温度剖面的类型,反过来一样。
流体微元内温度的不均匀分布给熵平衡方程带来更多的项。(17)式变为[5]:

(44) 可以看出这些额外项是温度梯度的平方项。在熵产生中,与温度和速度梯度相关的项是分离的,没有二者之间的耦合项。
因此,假设在转捩区间径向脉动速度ṽ的数值与完全湍流的一样时,合成流动的观点在有传热发生时一样成立。合成温度可以用类似(25)和(26)式的方式来定义,并且可以采用一个不同的序参数来描述传热类型的转变[22-23]。如果采用相同的序参数描述传热类型的转变,在平均熵产生中的额外项为:

(45) 其中层流和湍流变量的表示方法与(15)和(16)式中的一样。
可以看出对于传热类型的转变,可以类似地定义平均合成熵产生。在应用最小熵产生稳定性准则后,可以得到与(34)和(39)式相同的式子。不同的序参数,意味着对于流动和传热类型的转变,允许相似和独立的过程。这与实验结果一致。传热实验表明,温度剖面的自然转捩在ReL约为2300时开始,在ReR约为10 000时结束[20-21]。对于速度剖面的转捩,流动速度振荡的测量结果说明,ReL和ReR的差别要小得多[2]。
5 与实验结果的对比
5.1 常温水的轴对称流动
在文献[2, 8, 24]中,采用常温水进行了大量没有传热发生的管流实验,包括较多强迫转捩和少量自然转捩实验。由于Re正比于水的质量流量,不同Re的实验可以通过改变水的流量来进行。这样,可以方便地测得在ReL和ReR之间不同Re时轴向速度及其脉动的统计特性。本文的推导可以用来解释这些统计特性。
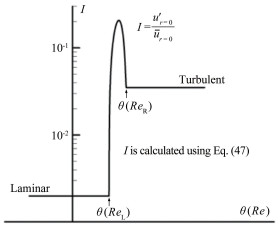
在同一Re下,层流速度u和湍流的平均速度u之间的差别,与湍流脉动值ũ相比在数值上是很大的。根据(30)式,在圆管内的转捩区间里,轴向速度脉动应该有过冲(Overshoot)现象。文献[2, 8, 24]清楚地测量了这种过冲现象。为了进行对比,可以通过(29)和(30)式来计算在中心线上(r等于0)轴向速度的脉动强度。脉动速度的方均根值u′及其脉动强度I为:

(46) 
(47) 为与实际流动进行对比,这里考虑了层流内速度的脉动强度(通常很小)。
为和自然转捩情形进行对比,选取文献[2]中图 3的数据进行计算,其中对于湍流,ur=0=1.4U和u′r=0=0.035ur=0,对于层流ur=0=2.0U和u′r=0=0.002ur=0。图 4给出了r=0处轴向速度脉动强度I的计算结果。
如图 4所示,(47)式给出中心线上I最大值为20.7%(在(39)式的θ等于0.07π时)。图 4中I的形状和数值可以与文献[2]的测量进行对比,在文献[2]中测量的最大值约为20%。在转捩区间轴向速度的脉动强度有时比湍流的5倍还大,这种大的过冲源于η的振荡。文献[2]还报道,这种轴向速度脉动的过冲现象,没有导致摩阻系数的过冲。本文推导也能解释这种现象。
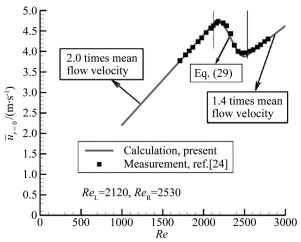
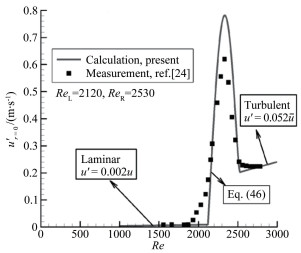
在文献[24]中给出了在强迫转捩区间内中心线上轴向速度及其脉动量统计平均的测量值,图 5和6是本文的计算结果与它们的比较。计算忽略了在全湍流中u′r=0/ur=0随Re的变化。从图 5可以看出,对于在转捩区间里中心线上的轴向速度,采用(29)式的计算与测量结果吻合很好。从图 6可以看出,对于在转捩区间里中心线上轴向脉动速度的统计平均值,采用(46)式的计算能够给出与实验测量大致一致的趋势和数值。扰动的振幅不同时,在湍流流动里轴向脉动速度的方均根值与平均速度的比值也会不同,在图 6的计算中取u′r=0=0.052ur=0(在图 4的计算中比例系数为0.035,两图的比例系数取自不同的实验)。
文献[7]提到一个“奇怪效应”(Strange Effect)。在管道流动实验中,对于层流和湍流,压力计的读数保持平稳,但是在转捩区间里压力计的读数剧烈震荡。这个现象能够采用在转捩区间里η的振荡来进行解释。
5.2 一个加热圆管内的转捩
为进行超燃冲压发动机的冷却设计,多年来碳氢化合物在电加热圆管内的流动和传热引起了一些兴趣[25-26]。如果较冷的流体自较热的表面流过,二者之间会发生对流传热。工程上采用Nusselt数(Nu)这个无量纲数来表示表面上对流传热的强弱。可以把Nu的定义式写为[20-21]:

(48) 其中q是表面上的热流,d是管子内径,Tw是表面温度,对于内部流动Tf是流体的平均温度。
传热关系式把Nu与Re和Prandtl数(Pr)联系起来,指的是下述关系式:

(49) 层流和湍流有显著不同的传热关系式,在工程应用里都可以当做通用关系式。在采用(48)式计算时,Tw的数值取决于Nu。因此,碳氢燃料的传热关系式对冷却通道的设计具有重要意义。
文献[27]采用电加热管对不同传热类型的Nu关系式进行了实验研究。通过测量电流、管子的电阻、流体的质量流量、管子直径和厚度、外壁温度以及流体在进出口的温度和压强,来确定传热关系式。在转捩区间发现Nu关系式的实验结果为[27]:

(50) 这表明在转捩区间里,NuTran形式上为相同Re下层流传热Nusselt数(NuLam)和湍流传热Nusselt数(NuTurb)的权重叠加,并且实验数据表明权重因子η与(39)式一样。文献[27]的数据在图 7中给出,其中Nu表达式采用的是这种权重叠加规律。
这个圆管内加热流动的独特之处,在于其中包含了完整的从层流到湍流的流动和传热类型的转变过程。在转变过程中,采用η来描述合成流动。在转捩区间流动和传热的演化,由从(35)式导出的(39)式来描述。(35)式确定的是η的振荡,不同形式的(35)式和不同的限制条件,会导致不同于(39)式的结果。从上述与实验现象的对比可以得出,对于圆管内的流动和对流传热,在转捩区间的振荡特性和转捩行为可以用本文的推导进行解释。在转捩过程中,η的振荡控制着转捩的演化,宏观振荡同时存在随机性和确定性的特点。
6 结论
轴对称层流到湍流的转捩和在转捩区间速度和温度的振荡,可以采用合成流动的观点、合成比例的振荡以及最小熵产生稳定性准则来进行解释。
(1) 假设在转捩区间径向脉动速度ṽ与充分发展区湍流中的径向脉动速度在数值上完全相同,在每个截面上的流动和传热可以分解为充分发展区的层流和湍流成分。两种成分的合成比例用来定义转捩区间的流动和传热。
(2) 在转捩区间合成比例会发生振荡,这种振荡控制着转捩行为。在转捩过程中,流体的轴向速度(和温度)的大的振荡,主要由合成比例的振荡引起。在宏观振荡中同时具有随机性和确定性的特点。
(3) 圆管内层流到湍流的转捩过程,可以与热力学平衡系统的连续相变进行比较。描述后者的序参数和振荡区间等概念,可以在前者的研究中采用。
(4) 对于在圆管内流动和传热类型的转变,允许相似和独立的过程。
-
表 1 二元混合物相变和圆管内流动转捩的对比
Table 1 Analogies between the phase transition of a binary mixture and the flow transition
系统 序参数 热力学函数 处理方法 二元混合物(平衡系统) 浓度x或其线性函数 自由能,混合自由能 混合自由能取极小值来确定x(Landau理论的精神) 一个截面上的流体微元(非平衡系统) 合成比例η或其线性函数 平均熵产生,平均合成熵产生 平均合成熵产生取极小值来确定η(利用了Landau理论的精神) -
[1] Mullin T. Experimental studies of transition to turbulence in a pipe[J]. Annual Review of Fluid Mechanics, 2011, 43:1-24. DOI: 10.1146/annurev-fluid-122109-160652
[2] Durst F, Ünsal B. Forced laminar-to-turbulent transition of pipe flows[J]. J Fluid Mech, 2006, 560:449-464. DOI: 10.1017/S0022112006000528
[3] Darbyshire A G, Mullin T. Transition to turbulence in constant-mass-flux pipe flow[J]. J Fluid Mech, 1995, 289:83-114. DOI: 10.1017/S0022112095001248
[4] Eckhardt B, Schneider T M, Hof B, et al. Turbulence transition in pipe flow[J]. Annual Review of Fluid Mechanics, 2007, 39:447-468. DOI: 10.1146/annurev.fluid.39.050905.110308
[5] Reichl L E. A modern course in statistical physics[M]. New Jersey:John Wiley & Sons Inc, 1998.
[6] Landau L D, Lifshitz E M. Statistical physics:part 1[M]. 3rd ed. Oxford:Pergamon Press, 1980.
[7] McComb W D. The physics of fluid turbulence[M]. Oxford:Claredon Press, 1992.
[8] Nishi M, Ünsal B, Durst F, et al. Laminar-to-turbulent transition of pipe flows through puffs and slugs[J]. J Fluid Mech, 2008, 614:425-446. DOI: 10.1017/S0022112008003315
[9] Henkel M, Hinrichsen H, Lübeck S. Non-equilibrium phase tran-sitions, Volume Ⅰ:Absorbing phase transitions[M]. Netherlands:Canopus Academic Publishing Limited, 2008.
[10] Cowan B. Topics in statistical mechanics[M]. London:Imperial College Press, 2005.
[11] Huang K. Statistical mechanics[M]. New Jersey:John Wiley & Sons Inc, 1987.
[12] Landau L D, Lifshitz E M. Fluid mechanics[M]. 2nd ed. Oxford:Pergamon Press, 1987.
[13] Eckert E R G, Drake R M Jr. Analysis of heat and mass transfer[M]. Tokyo:McGraw-Hill Kogakusha Ltd, 1972.
[14] Koch H, Tataru D. Well-posedness for the Navier-Stokes equations[J]. Adv Math, 2001, 157(1):22-35. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1302.5785
[15] Durmagambetov A A, Fazilova L S. Navier-Stokes equations-millennium prize problems[J]. Natural Science, 2015, 7(2):54262. http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0215037970/
[16] Lifshitz E M, Pitaevskii L P. Statistical physics:part 2[M]. Oxford:Pergamon Press, 1980.
[17] Glansdorff P, Prigogine I. Structure, stability, and fluctuations[M]. New Jersey:Wiley-Interscience, 1971.
[18] Nicolis P, Prigogine I. Self-organization in nonequilibrium systems[M]. New Jersey:Wiley-Interscience, 1977.
[19] Prigogine I. Time, structure, and fluctuations[J]. Science, 1978, 201:777-785. DOI: 10.1126/science.201.4358.777
[20] Bergman T L, Lavine A S, Incropera F P, et al. Fundamentals of heat and mass transfer[M]. 7th ed. New Jersey:John Wiley & Sons Inc, 2011.
[21] Rohsenow W M, Hartnett J P, Cho Y I. Handbook of heat transfer[M]. 3rd ed. New York:McGraw-Hill Book Company, 1998.
[22] Zhang R L, Le J L. Natural laminar-to-turbulent transition inside an electrically heated circular tube[C]//Proc of AIP Conference Proceedings 1770: 030035. 2016.
[23] 张若凌, 乐嘉陵.电加热圆管内流动的自然转捩过程研究[J].实验流体力学, 2017, 31(2):51-60. http://www.syltlx.com/CN/abstract/abstract11011.shtml Zhang R L, Le J L. Natural laminar-to-turbulent transition inside an electrically heated circular tube[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(2):51-60. http://www.syltlx.com/CN/abstract/abstract11011.shtml
[24] Nishi M. Laminar to turbulent transition in pipe flow through puffs and slugs[D]. Der Technischen Fakultät der Friedrich-Alexander-Universität Erlangen-Nürnberg, 2009.
[25] Linne D L, Meyer M L, Edwards T, et al. Evaluation of heat transfer and thermal stability of supercritical JP-7 fuel[R]. AIAA-97-3041, 1997.
[26] Huang H, Sobel D R, Spadaccini L J. Endothermic heat-sink of hydrocarbon fuels for scramjet cooling[R]. AIAA-2002-3871, 2002.
[27] Zhang L, Zhang R L, Xiao S D, et al. Researches on heat transfer correlations of hydrocarbon fuel under supercritical pressure[J]. International Journal of Heat and Mass Transfer, 2013, 64:393-400. DOI: 10.1016/j.ijheatmasstransfer.2013.04.058
-
期刊类型引用(2)
1. 王亚龙,朱潇潇. 基于圆柱绕流分析k-ε和k-w湍流模型的差异. 机电产品开发与创新. 2022(02): 13-16 .  百度学术
百度学术
2. 赵波,刘建,李开勇. 纵掠平板速度和温度边界层湍流转捩区的积分方法. 四川大学学报(自然科学版). 2021(03): 137-146 .  百度学术
百度学术
其他类型引用(2)






 下载:
下载: