尖前缘驻点热流精细化测量研究

张杨; 贾广森; 沙心国; 陈星

doi:10.11729/syltlx20180112

尖前缘驻点热流精细化测量研究

张杨^1,,
贾广森²,
沙心国^2, ,,
陈星²

1.
北京航天长征飞行器研究所, 北京 100076
2.
中国航天空气动力技术研究院, 北京 100074

基金项目:

国家自然科学基金面上项目 11872349，91752111

详细信息

作者简介:
张杨(1978-), 女, 湖南醴陵人, 高级工程师, 硕士研究生。研究方向:气动热环境研究。通信地址:北京9200信箱76分箱9号。E-mail:zhangy1zy@sina.com

通讯作者:
沙心国, E-mail: shaxg@163.com

中图分类号: V211.71
计量
- 文章访问数: 198
- HTML全文浏览量: 98
- PDF下载量: 17
出版历程
- 收稿日期: 2018-08-24
- 修回日期: 2018-12-24
- 刊出日期: 2019-12-24

Precise stagnation point heat flux measurement technique of sharp leading edges

1.
Beijing Institute of Space Long March Vehicle, Beijing 100076, China
2.
China Academy of Aerospace Aerodynamics, Beijing 100074, China

摘要

摘要: 为提高升阻比特性，现代高超声速飞行器常采用尖前缘结构，这对热防护系统提出了很大挑战。尖前缘结构由于表面曲率较大，常规的点测量和面测量试验技术均难以对驻点热流进行准确测量。针对尖前缘驻点热流测量难题，制作了专用的整体式薄膜电阻温度计，建立了驻点热流参数辨识方法，并以不同前缘半径（R=1.0、2.0和5.0 mm）的斜劈模型为研究对象，在FD-20高超声速脉冲风洞中开展了试验验证，来流马赫数分别为4、5、6和8，试验结果表明：整体式传感器稳定性好、灵敏度高、耐冲刷性强，其参数辨识方法精度高，试验获得的前缘驻点热流与理论值误差小于15%。
- 尖前缘 /
- 驻点热流 /
- 风洞试验 /
- 参数辨识
Abstract: In order to improve the aerodynamic performance, a sharp leading edge is widely used in the hypersonic flight vehicles, which exerts a huge challenge on thermal protection systems. The sharpness of the leading edge makes it hard to measure the stagnation point heat flux precisely. In this paper, an integral sensor with high spatial resolution is developed to measure the stagnation point heat flux, and the corresponding estimation method is adopted as well. A wedge model with an interchangeable nose(R=1.0, 2.0 and 5.0 mm) is employed to validate the effectiveness of the sensor, and a series of experiments are conducted at the FD-20 impulse wind tunnel under the condition of Mach number of 4, 5, 6 and 8. The results indicate that the difference of the stagnation point heat flux values is less than 15% between experimental measurement and theoretical prediction.
- sharp leading edges /
- stagnation point heat flux /
- wind tunnel testing /
- parameter identification

HTML全文

0 引言

随着新型耐高温材料的出现和防热技术的发展, 现代新型高超声速飞行器在追求大升阻比和高机动性的过程中逐渐开始采用尖前缘结构^[1-2]。但尖前缘结构会带来热流密度大, 防热困难的问题, 另外, 新型高超声速飞行器为保持高升阻比特性, 需要维持外形, 采用的非烧蚀热防护技术对尖前缘部位的热环境预测精度提出了更高的要求。

高超声速气动热测量试验主要在激波风洞中进行, 该类型风洞具有运行时间短、模型振动大的特点。因此对气动热测量技术提出了响应快、温升大、对模型振动不敏感的要求。气动热测量试验技术主要分为两类:一类是点测量技术, 包括薄膜电阻温度计^[3-4]、热电偶^[5]和量热计^[6]等; 另一类是面测量技术, 包括红外热图技术^[7]、温敏漆技术^[8]和磷光热图技术^[9]等。面测量技术可直观地显示飞行器模型表面温度和热流分布情况。但尖前缘结构存在涂层喷涂、光路布置双重困难, 以及模型振动会严重影响光学测量精度的问题, 因此尖前缘驻点热流测量还是主要依靠响应快的薄膜电阻温度计和同轴热电偶。

常用的薄膜电阻温度计和同轴热电偶通常为圆柱形。德国亚琛工业大学研制的镍铬-康铜同轴热电偶最小直径约为1.9 mm^[10]。而美国Calspan实验室研制的薄膜电阻温度计, 其直径为1.0 mm^[11], 是目前欧美国家制造出的尺寸最小的圆柱形热流传感器。国内中国航天空气动力技术研究院的薄膜电阻温度计最小直径为1.5 mm, 中国科学院力学研究所和中国航天空气动力技术研究院的同轴热电偶直径仅为1.4 mm^[12]。中国空气动力研究与发展中心开展了直径1.0 mm的薄膜电阻温度计和同轴热电偶技术研究^[13]。虽然热流传感器的尺寸越来越小, 但是依旧无法满足激波风洞中缩比模型尖前缘驻点热流精细化测量的需求。2011年陈星等发展了一种具有更高空间分辨率的型面状薄膜电阻温度计, 其敏感元件宽约0.1 mm, 长1.3 mm, 可用于R=1.0 mm前缘驻点热流测量^[14-15]。中国科学院力学研究所的吴松等提出一种整体式热电偶传感器的设计思想, 该传感器电偶丝的最小直径仅0.1 mm, 可以满足R=0.5 mm驻点热流的测量需求^[16]。

近年来, 国内针对尖前缘驻点热流测量发展的整体式热流传感器, 可以满足最小前缘半径R=0.5 mm的驻点热流测量需求。由于驻点热流与半径的平方根成反比, 前缘半径越小, 驻点热流越高, 模型前缘温升越大, 传感器基底材料热物性参数随温度的变化影响越来越大, 另外, 尖前缘部位曲率大, 三维热传导的影响也需要考虑, 如何由整体式传感器直接测量获得的温度数据准确辨识驻点热流仍是一个难题。为此, 本文开展尖前缘驻点热流精细化测量试验技术研究, 制作了专用的尖前缘驻点热流测量传感器, 建立了尖前缘驻点热流辨识方法, 并以不同前缘半径的斜劈模型为研究对象在高超声速脉冲风洞中开展了风洞验证试验。

1 传感器研制

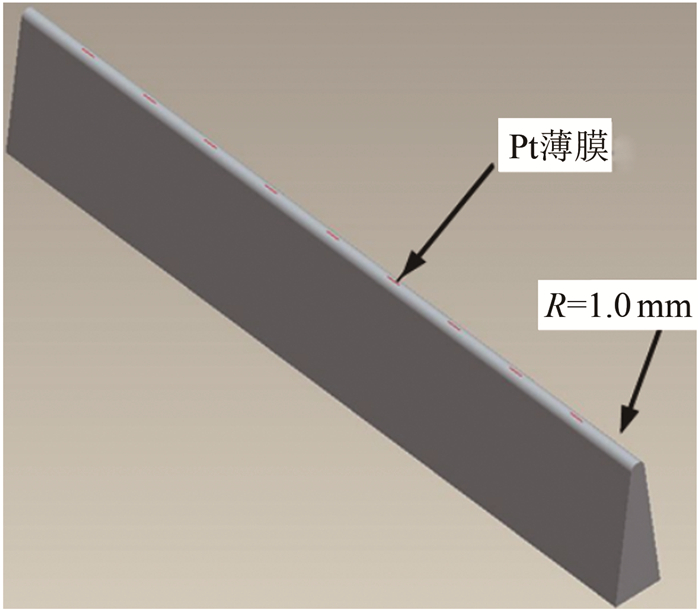
为解决传感器测量端面对前缘型面的破坏, 采用一体化技术将薄膜电阻温度计与模型结合到一起, 在尖前缘外形的玻璃基底上进行镀膜, 制成整体式传感器。用于热流测量的温敏铂薄膜长度为2.0 mm, 宽度为0.2 mm, 薄膜长度方向与前缘纵向一致, 如图 1和2所示, 由于无后掠二维前缘驻点热流沿长度方向不发生变化, 因此在前缘无后掠的情况下, 薄膜长度对驻点热流测量没有影响。按连续流Lees二维圆柱热流计算公式^[17], 对于R=1.0 mm前缘, 0.2 mm宽的薄膜所覆盖的前缘周向角为11.5°, 薄膜宽度引起的热流测量误差小于0.2%, 可以忽略。上述分析表明, 整体式传感器以及沿前缘长度方向镀膜的方案满足尖前缘驻点热流测量的需要。

图 1 尖前缘驻点热流测量传感器示意图

Fig. 1 Schematic of the integral heat flux sensors

下载: 全尺寸图片幻灯片

图 2 尖前缘驻点热流测量传感器实物图

Fig. 2 Photograph of the integral heat flux sensors

下载: 全尺寸图片幻灯片

2 数据处理方法

现有风洞气动热试验热流数据后处理方法多采用基于一维半无限大假设的Cook-Felderman公式^[18], 通过数值积分的方法获得传感器表面热流, 如式(1)所示。

(1)

其中, ρ、c、k分别为基底材料的热物性参数密度、比热容和导热系数。

在尖化前缘区域热流值高, 表面曲率变化大。由于热流较高, 在相同的试验时间内, 基底温升较高, 基底材料的热物性会随着基底材料温度的升高而发生较大变化, 其变化对最终热流的计算会产生重大的影响。此外, 对于尖前缘及局部曲率变化大的地方, 存在严重的三维导热现象, 而目前国内在测热数据后处理上多基于一维半无限大假设原理, 采用Cook-Felderman方法, 该方法没有考虑热物性参数的变化及三维导热现象对试验结果的影响。而这2种因素在高热流、大曲率下为影响测热精度的重要因素。

2.1 热物性参数变化影响

随着温度的变化, 材料的热物性会发生显著的变化, 文献^[19]指出材料的热物性是影响测量结果的重要因素。式(1)热流计算中假设基底材料的热物性在试验过程中为一常数, 忽略了热物性的变化, 该假设在温升小的情况下误差较小。但在一些气动加热严重, 温升高的区域(比如激波干扰区、尖化前缘驻点等), 传感器的基底材料热物性变化较大, 会对试验测量精度产生重要的影响。

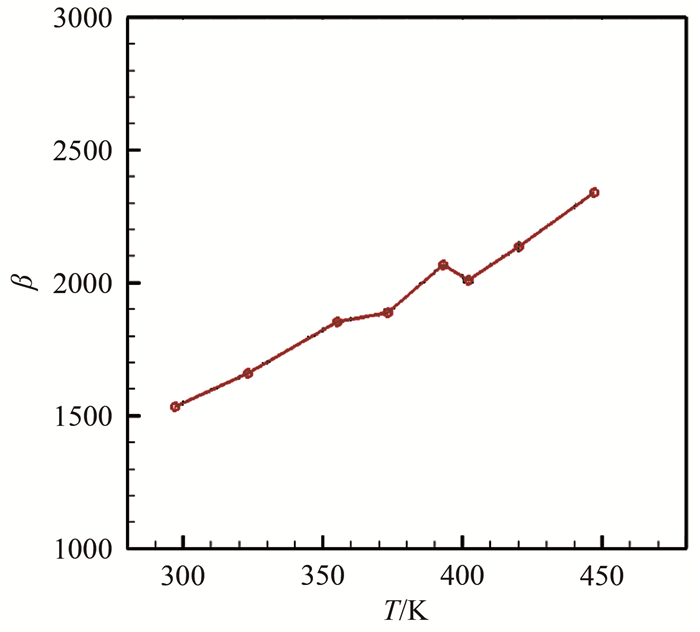
目前在中国航天空气动力技术研究院高超声速脉冲风洞中所采用的整体式传感器基底材料为高硼硅酸玻璃, 文献^[20]给出了该基底材料的热物性参数随温度的变化情况, 如图 3所示。

图 3 热物性随温度的变化规律

Fig. 3 Substrate thermal property variation with temperature

下载: 全尺寸图片幻灯片

由图可知, 随着传感器表面温度的升高, 基底材料的热扩散率逐渐增大, 在表面温度为100 K时, 集中热物性的变化在50%以上。因此风洞试验中, 在一些温度升高较大的区域, 基底材料热物性变化显著, 须考虑基底材料热物性变化对测量结果的影响。

随着基底材料热扩散率的增加, 在相同的热流作用下, 材料表面温升将有所降低。采用现有的热流计算方法分别计算常物性和变物性2种工况下的热流值, 如图 4所示。可以看出, 按照现有热流后处理方法, 随着表面温度的变化, 热流计算结果会带来较大的误差。在表面温度升高100 K以上时, 热流计算误差已在10%以上, 因此在热流测量中, 尤其是在大温升的地方, 必须改进现有的数据后处理方法。

图 4 热物性参数对热流测量的影响

Fig. 4 Heat flux deviation with temperature rise

下载: 全尺寸图片幻灯片

2.2 多维热传导影响

Cook-Felderman公式是基于一维半无限大假设得出的, 忽略了周向热传导, 认为热量只沿着壁厚方向传导。但是在尖前缘位置, 前缘半径很小, 周向导热不能忽略, 该假设已不再适用, 必须考虑三维热传导对热流计算的影响。为此采用有限元数值计算的方法, 针对研制的整体式热流传感器, 研究了多维热传导对热流计算结果的影响。

在笛卡尔坐标系下, 多维非稳态导热方程(忽略源项)如下:

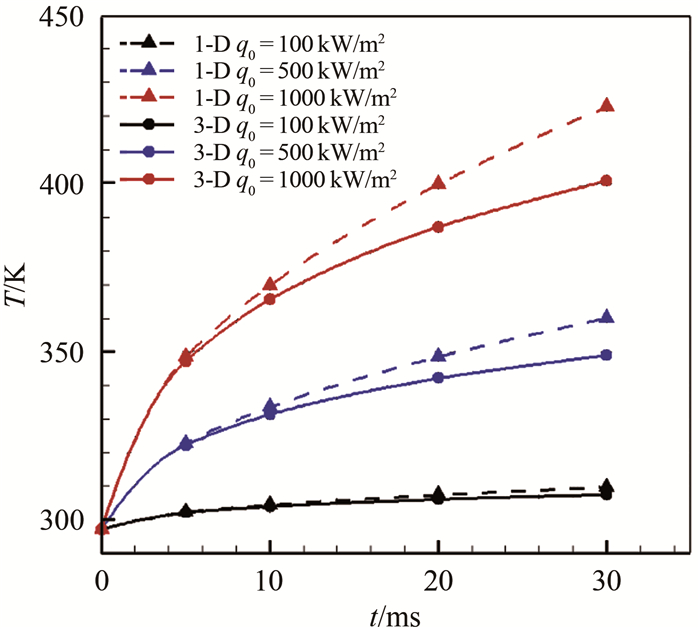
(2)

采用有限体积法的离散格式, 研究了前缘半径和试验时间对热流计算结果的影响。基底材料初始温度为297.15 K, 图 5为加载不同热流条件下半径1 mm的前缘表面温升。从图 5可以看出, 随着加热时间的增加, 采用一维热传导和三维热传导计算获得的表面温升差距越来越大, 因此加热时间越长三维热传导现象越严重; 在前缘加载30 ms的1000 kW/m²热流, 采用一维热传导和三维热传导计算获得的模型表面温差超过了20 K。因此, 在前缘热流测量中, 三维热传导现象不能忽略。

图 5 不同来流条件下表面温升(前缘半径R=1 mm)

Fig. 5 Computed temperature rise under various flow conditions

下载: 全尺寸图片幻灯片

表 1为在不同热流条件下, 根据传感器表面温升, 分别采用Cook-Felderman公式和三维热传导的数据处理方法计算获得的模型表面热流。对比可知, 不同热流条件下, 在同一时刻, 三维热传导现象对热流计算的影响相同, 这说明三维热传导的影响只与模型的几何尺寸及加热时间有关, 与来流条件无关。随着加热时间的增加, 三维热传导的影响越来越大。

表 1 不同来流条件测量误差随计算时间变化情况

Table 1 Measured heat flux error deviation with time under various flow conditions

Q/(kW·m^-2)	Time/ms	Q_1D/Q_3D^*
100	5	0.976
	10	0.942
	20	0.876
	30	0.825
500	5	0.976
	10	0.942
	20	0.876
	30	0.825
1000	5	0.976
	10	0.942
	20	0.876
	30	0.825
^*: Q_1D采用一维热传导计算值, Q_3D采用三维热传导计算值。

下载: 导出CSV

| 显示表格

为了研究几何尺寸对三维热传导的影响, 对不同前缘半径模型的驻点热流进行了计算, 结果如图 6所示。对比可知, 在相同的热流条件下, 随着前缘半径的减小, 模型前缘表面温升越来越低, 三维热传导越来越严重。

图 6 前缘半径对多维导热的影响

Fig. 6 Computed temperature versus time for different sharp leading edge radiuses

下载: 全尺寸图片幻灯片

多维热传导的影响程度与模型前缘半径大小和试验时间有关, 在相同的试验时间内, 前缘半径越小, 三维热传导的影响越大。对于同一前缘半径, 随着试验时间的增加, 三维热传导的影响越来越大。

2.3 数据修正方法

通过上述分析可知, 尖前缘驻点热流测量试验中, 前缘半径较小, 驻点区域热流较大, 温升较高。试验过程中传感器基底材料热物性参数变化大, 三维热传导现象比较严重。因此, 这2个因素对热流的影响较大, 不能再忽略。对于非线性多维热传导的计算方法很多, 但是能运用到工程实际中, 可快速计算出热流值指导试验的很少。本文在原有Cook-felderman公式的基础上引入修正因子Φ, 其中Φ是与模型表面温升、前缘半径和试验时间相关的量。此时热流计算公式可以转化为:

(3)

式中, Φ=185.61(13.3τ+0.6)R^-0.27T^-0.25, τ为试验时间, R为前缘半径, T是表面温升(由薄膜电阻温度计测得)。

为了对比试验数据, 采用经典的Fay-Riddell驻点热流计算公式^[21]对二维楔面模型前缘驻点热流进行理论计算:

(4)

其中q_2D为二维楔面模型前缘驻点热流, q_R为相同半径球头驻点热流(球头驻点热流采用Fay-Riddell公式计算)。

3 风洞验证试验

为了验证传感器的性能和数据处理方法的精度, 以前缘半径分别为1、2和5 mm的斜楔模型(见图 7)为研究对象, 开展不同半径前缘驻点热流的测量试验。来流实际马赫数为4.02、4.92、5.92和7.97, 试验在中国航天空气动力技术研究院(CAAA)的FD-20高超声速脉冲风洞(见图 8)中进行, 该风洞有2种不同的运行方式:带有活塞和不带活塞, 采用整体式薄膜电阻温度计进行驻点热流测量。

图 7 斜劈模型

Fig. 7 Wedge model

下载: 全尺寸图片幻灯片

图 8 FD-20脉冲风洞

Fig. 8 FD-20 impulse wind tunnel

下载: 全尺寸图片幻灯片

来流总压由安装在前室管壁上的压力传感器测出, 总温根据理想激波管理论和等熵关系式计算得出, 其他流场参数是假定气流在喷管中作等熵膨胀计算得出的, 具体来流参数如表 2所示。

表 2 试验来流参数

Table 2 Test conditions

Flow condition	Ma	p_o/MPa	T_o/K	Re/m^-1	Piston
(1)	4.02	2.00	624.7	2.92×10⁷	NO
(2)	4.92	3.08	631.6	2.81×10⁷	NO
(3)	5.92	6.56	909.7	2.21×10⁷	YES
(4)	7.97	19.36	960.0	2.83×10⁷	YES

下载: 导出CSV

| 显示表格

表 3为不同来流条件下, 不同前缘半径模型驻点热流试验测量值、理论值及误差分布。对比可知, 在相同来流条件下, 驻点热流随着前缘半径的增加而逐渐减小。在来流条件(1), 前缘半径R=1 mm时, 驻点热流测量误差为-14.79%;前缘半径R=2 mm时, 驻点热流测量误差为-2.63%;而前缘半径增大到R=5 mm时, 驻点热流测量值比理论值大, 测量误差为+7.26%, 该规律与文献[4]规律一致, 随着前缘半径的增加, 驻点热流测量值逐渐由小于理论值变为大于理论值。

表 3 不同来流条件下尖前缘驻点热流测量结果及误差

Table 3 Measured heat flux and errors

Flowcondition		R=1 mm	R=2 mm	R=5 mm
(1)	Q_t/(kW·m^-2)	1154.5	816.3	516.3
	Q_exp/(kW·m^-2)	983.7	794.9	553.8
	Error	-14.79%	-2.63%	+7.26%
(2)	Q_t/(kW·m^-2)		721.0
	Q_exp/(kW·m^-2)		676.4
	Error		-6.19%
(3)	Q_t/(kW m^-2)	1921.2	1358.5	859.2
	Q_exp/(kW·m^-2)	1097.0	956.4	676.2
	Error	-42.9%	-29.6%	-21.3%
(4)	Q_t/(kW·m^-2)		1331.8
	Q_exp/(kW·m^-2)		952.4
	Error		-28.49%
Error=(Q_exp-Q_t)/Q_t×100%, Q_t为理论值, Q_exp为试验测量值, Q_exp.m为修正后的试验测量值

下载: 导出CSV

| 显示表格

对比不同来流条件下相同前缘半径的驻点热流测量误差可以看出, 在来流条件(1)和(2)下, 驻点热流测量误差均小于15%, 而在来流条件(3)和(4)下, 驻点热流测量误差明显增大。在来流条件(3)下, R=1 mm时, 驻点热流测量误差高达-42.9%。造成这种差异的主要原因是风洞运行方式不同, 来流条件(1)和(2)使用的是激波风洞运行方式, 试验中不使用活塞, 试验气流的总压和总温提高是通过激波压缩实现的, 而来流条件(3)和(4)采用的是炮风洞运行方式, 试验中采用活塞压缩来提高气流的总压和总温。不同的风洞运行方式建立有效流场经历的时间不同, 从而使得驻点位置三维热传导程度和传感器基底材料的热物性参数变化程度不同。炮风洞运行方式建立有效流场需要经历的时间明显高于激波风洞运行方式, 使得驻点位置三维热传导程度和传感器基底材料的热物性参数变化明显高于激波风洞运行方式, 从而造成炮风洞运行方式测量获得的驻点热流明显小于理论值, 因此需要对炮风洞运行方式下驻点热流的测量值进行修正。

采用式(3)的数据处理方法对炮风洞运行方式下的驻点热流测量结果进行了修正, 数据修正前后对比如表 4所示, 经过该方法修正后的驻点热流数据与理论值的误差在10%以内, 说明使用该数据处理方法处理高超声速炮风洞驻点热流测量结果具有较高的精度。

表 4 修正前后测量结果对比

Table 4 Comparison of measured and modified heat flux

Flow condition		R=1 mm	R=2 mm	R=5 mm
(3)	Q_t/(kW·m^-2)	1921.2	1358.5	859.2
	Q_exp/(kW·m^-2)	1097.0(-42.9%)	956.4(-29.6%)	676.2(-21.3%)
	Q_exp.m/(kW·m^-2)	1808.7(-5.86%)	1339.2(-1.42%)	817.6(-4.84%)
(4)	Q_t/(kW·m^-2)		1331.8
	Q_exp/(kW·m^-2)		952.4(-28.49%)
	Q_exp.m/(kW·m^-2)		1322.93(-0.67%)

下载: 导出CSV

| 显示表格

4 结论

针对尖前缘驻点热流测量难题, 制作了整体式传感器, 对影响尖前缘驻点热流测量精度的主要因素进行了分析, 获得了传感器基底材料热物性参数变化和三维热传导现象对试验测量结果的影响, 提出了一种新的试验数据修正方法。最后, 以不同前缘半径斜劈模型为研究对象, 开展了风洞验证试验。通过分析与对比, 得到以下结论:

(1) 随着传感器表面温度的升高, 基底材料的热扩散率逐渐增加, 从而使得传感器基底材料的温升减小, 热流测量结果偏低。

(2) 在尖前缘位置, 由于前缘半径很小, 模型表面不再满足一维半无限大假设, 须考虑三维热传导的影响。

(3) 模型表面的三维热传导对驻点热流测量结果的影响只与模型的几何尺寸及试验时间有关, 与来流条件无关。前缘半径越小, 风洞运行时间越长, 三维热传导的影响程度越大。

(4) 基于试验时间、前缘半径和表面温升的数据修正方法进行尖前缘驻点热流数据的修正具有较高的精度。

图 1 尖前缘驻点热流测量传感器示意图

Fig. 1 Schematic of the integral heat flux sensors

下载: 全尺寸图片幻灯片

图 2 尖前缘驻点热流测量传感器实物图

Fig. 2 Photograph of the integral heat flux sensors

下载: 全尺寸图片幻灯片

图 3 热物性随温度的变化规律

Fig. 3 Substrate thermal property variation with temperature

下载: 全尺寸图片幻灯片

图 4 热物性参数对热流测量的影响

Fig. 4 Heat flux deviation with temperature rise

下载: 全尺寸图片幻灯片

图 5 不同来流条件下表面温升(前缘半径R=1 mm)

Fig. 5 Computed temperature rise under various flow conditions

下载: 全尺寸图片幻灯片

图 6 前缘半径对多维导热的影响

Fig. 6 Computed temperature versus time for different sharp leading edge radiuses

下载: 全尺寸图片幻灯片

图 7 斜劈模型

Fig. 7 Wedge model

下载: 全尺寸图片幻灯片

图 8 FD-20脉冲风洞

Fig. 8 FD-20 impulse wind tunnel

下载: 全尺寸图片幻灯片

表 1 不同来流条件测量误差随计算时间变化情况

Table 1 Measured heat flux error deviation with time under various flow conditions

Q/(kW·m^-2)	Time/ms	Q_1D/Q_3D^*
100	5	0.976
	10	0.942
	20	0.876
	30	0.825
500	5	0.976
	10	0.942
	20	0.876
	30	0.825
1000	5	0.976
	10	0.942
	20	0.876
	30	0.825
^*: Q_1D采用一维热传导计算值, Q_3D采用三维热传导计算值。

下载: 导出CSV

表 2 试验来流参数

Table 2 Test conditions

Flow condition	Ma	p_o/MPa	T_o/K	Re/m^-1	Piston
(1)	4.02	2.00	624.7	2.92×10⁷	NO
(2)	4.92	3.08	631.6	2.81×10⁷	NO
(3)	5.92	6.56	909.7	2.21×10⁷	YES
(4)	7.97	19.36	960.0	2.83×10⁷	YES

下载: 导出CSV

表 3 不同来流条件下尖前缘驻点热流测量结果及误差

Table 3 Measured heat flux and errors

Flowcondition		R=1 mm	R=2 mm	R=5 mm
(1)	Q_t/(kW·m^-2)	1154.5	816.3	516.3
	Q_exp/(kW·m^-2)	983.7	794.9	553.8
	Error	-14.79%	-2.63%	+7.26%
(2)	Q_t/(kW·m^-2)		721.0
	Q_exp/(kW·m^-2)		676.4
	Error		-6.19%
(3)	Q_t/(kW m^-2)	1921.2	1358.5	859.2
	Q_exp/(kW·m^-2)	1097.0	956.4	676.2
	Error	-42.9%	-29.6%	-21.3%
(4)	Q_t/(kW·m^-2)		1331.8
	Q_exp/(kW·m^-2)		952.4
	Error		-28.49%
Error=(Q_exp-Q_t)/Q_t×100%, Q_t为理论值, Q_exp为试验测量值, Q_exp.m为修正后的试验测量值

下载: 导出CSV

表 4 修正前后测量结果对比

Table 4 Comparison of measured and modified heat flux

Flow condition		R=1 mm	R=2 mm	R=5 mm
(3)	Q_t/(kW·m^-2)	1921.2	1358.5	859.2
	Q_exp/(kW·m^-2)	1097.0(-42.9%)	956.4(-29.6%)	676.2(-21.3%)
	Q_exp.m/(kW·m^-2)	1808.7(-5.86%)	1339.2(-1.42%)	817.6(-4.84%)
(4)	Q_t/(kW·m^-2)		1331.8
	Q_exp/(kW·m^-2)		952.4(-28.49%)
	Q_exp.m/(kW·m^-2)		1322.93(-0.67%)

下载: 导出CSV

参考文献(21)

[1]	姜贵庆, 张学军, 王淑华, 等.飞行器尖化前缘的热结构特性[J].宇航材料工艺, 2007, 37(4): 8-11. DOI: 10.3969/j.issn.1007-2330.2007.04.003 Jiang G Q, Zhang X J, Wang S H, et al. Thermal structure properties of sharp leading edges for spacecraft[J]. Aerospace Materials and Technology, 2007, 37(4): 8-11. DOI: 10.3969/j.issn.1007-2330.2007.04.003
[2]	Salute J, Bull J, Rasky D, et al. SHARP-B2: flight test objectives, project implementation and initial results[C]//Proc of the 2nd Annual Conference on Composites, Materials and Structures. 2001.
[3]	曾磊, 石友安, 孔荣宗, 等.薄膜电阻温度计原理性误差分析及数据处理方法研究[J].实验流体力学, 2011, 25(1): 79-83. DOI: 10.3969/j.issn.1672-9897.2011.01.016 Zeng L, Shi Y A, Kong R Z, et al. Study on principle error analysis and data processing method of thin film resistance thermometer[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(1): 79-83. DOI: 10.3969/j.issn.1672-9897.2011.01.016
[4]	Chadwick K M.Stagnation heat transfer measurement techni-ques in hypersonic shock tunnel flows over spherical segments[R]. AIAA-97-2493, 1997.
[5]	Gai S, Baird J, Lyons P, et al. Stagnation point heat transfer in hypersonic high enthalpy flow[R]. AIAA-85-973, 1985.
[6]	Kidd C T.High heat flux measurements and experimental calibrations/characteriszations[C]//Proc of the 1992 NASA Langley Measurement Technology Conference: Measurement Technology for Aerospace Applications in High-Temperature Environments. 1992.
[7]	Juliano T J, Schneider S P. Instability and transition on the HIFiRE-5 in a Mach-6 quiet tunnel[R]. AIAA-2010-5004, 2010.
[8]	Sweeney C J, Chynoweth B C, Edelman J B, et al. Instability and transition experiments in the Boeing/AFOSR Mach 6 quiet tunnel[R]. AIAA-2016-0355, 2016.
[9]	毕志献, 韩曙光, 伍超华, 等.磷光热图测热技术研究[J].实验流体力学, 2013, 27(3): 87-92. DOI: 10.3969/j.issn.1672-9897.2013.03.017 Bi Z X, Han S G, Wu C H, et al. Phosphor thermography study in gun tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(3): 87-92. DOI: 10.3969/j.issn.1672-9897.2013.03.017
[10]	Wang Q, Olivier H, Einhoff J, et al. Influence of test model material on the accuracy of transient heat transfer measurements in impulse facilities[J]. Experimental Thermal and Fluid Science, 2019, 104: 59-66. DOI: 10.1016/j.expthermflusci.2019.02.013
[11]	Holden M S, Wadhams T P. A database of aerothermal measure-ments in hypersonic flow in 'building block' experi-ments for CFD validation[R]. AIAA-2003-1137, 2003.
[12]	张仕忠, 陈宏, 董志成, 等.高焓激波管驻点热流率测量[C]//第十四届全国激波与激波管学术会议论文集. 2010. Zhang S Z, Chen H, Dong Z C, et al. Heat-flux measurement at stagnation point in high-enthalpy shock tubes[C]//Proc of the 14th Chinese National Symposium on Shock Waves. 2010.
[13]	秦峰, 何川, 曾磊, 等.驻点热流测量试验技术研究[J].西南交通大学学报. 2013, 48(6): 1072-1077. DOI: 10.3969/j.issn.0258-2724.2013.06.016 Qin F, He C, Zeng L, et al. Experimental research of heat-transfer measurements on stagnation points[J]. Journal of Southwest Tiaotong University. 2013, 48(6): 1072-1077. DOI: 10.3969/j.issn.0258-2724.2013.06.016
[14]	陈星.尖化前缘热环境实验技术研究[D].长沙: 国防科学技术大学, 2011. Chen X. Experimental technique study of heat transfer measurement on sharp leading edges[D]. Changsha: National University of Defense Technology, 2011.
[15]	陈星, 宫建, 师军, 等.尖前缘驻点热流测量试验研究[C]//第十五届全国激波与激波管学术会议论文集. 2012. Chen X, Gong J, Shi J, et al. Experimental study of stagnation-point heat transfer measurement on sharp leading edges[C]//Proc of the 15th Chinese National Symposium on Shock Waves. 2012.
[16]	吴松, 舒勇华, 李进平, 等.一种具有时空高分辨率的整体式热流传感器[J].科学通报, 2014, 59(25): 2484-2489. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kxtb201425005 Wu S, Shu Y H, Li J P, et al. An integral heat flux sensor with high spatial and temporal resolutions[J]. Chinese Science Bulletin, 2014, 59(25): 2484-2489. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=kxtb201425005
[17]	Lees L. Laminar heat transfer over blunt-nosed bodies at hypersonic flight speed[J]. Jet Propulsion, 1956, 26(4): 259-269. DOI: 10.2514/8.6977
[18]	Cook W J, Felderman E J. Reduction of data from thin-film heat-transfer gages: a concise numerical technique[J]. AIAA Journal, 1996, 4(3): 561-562. http://cn.bing.com/academic/profile?id=2dc51f228f3971e6892a29b23c6e35c4&encoded=0&v=paper_preview&mkt=zh-cn
[19]	Dowding K, Beck J, Ulbrich A, et al. Estimation of thermal properties and surface heat flux in a carbon-carbon composite[J]. Journal of Thermophysics and Heat Transfer, 1995, 9(2): 345-351. DOI: 10.2514/3.666
[20]	Hartunian R A, Varwig R L. On thin-film heat-transfer measurements in shock tubes and shock tunnels[J]. Physics of Fluids, 1962, 5(2): 169-174. DOI: 10.1063/1.1706592
[21]	Fay J A, Riddell F R. Theory ofstagnation point heat transfer in dissociated air[J]. Journal of the Aeronautical Sciences, 1958, 25(2):73-85. https://www.researchgate.net/publication/312577255_Theory_of_Stagnation_Point_Heat_Transfer_in_Dissociated_Air

施引文献(2)

期刊类型引用(1)

朱新新，李泽禹，赵文峰，王辉，杨凯，杨庆涛. 水卡量热计的流热耦合模拟研究及试验分析. 实验流体力学. 2022(06): 83-88 .

本站查看

其他类型引用(1)

资源附件(0)

图(8) / 表(4)

计量

文章访问数: 198
HTML全文浏览量: 98
PDF下载量: 17
被引次数: 2

0 引言
1 传感器研制
2 数据处理方法
2.1 热物性参数变化影响
2.2 多维热传导影响
2.3 数据修正方法
3 风洞验证试验
4 结论

尖前缘驻点热流精细化测量研究

作者简介: 张杨(1978-), 女, 湖南醴陵人, 高级工程师, 硕士研究生。研究方向:气动热环境研究。通信地址:北京9200信箱76分箱9号。E-mail:zhangy1zy@sina.com

通讯作者: 沙心国, E-mail: shaxg@163.com

计量

出版历程

Precise stagnation point heat flux measurement technique of sharp leading edges