Hypersonic boundary layer transition simulation of complex configuration using γ-Reθ transition model
-
摘要: 在大规模并行可压缩Navier-Stokes求解器AHL3D框架上，搭建了γ-Reθ转捩模型。在该模型基础上，通过高超声速二维进气道构型算例，加入了可压缩性修正，使其能够模拟可压缩性对转捩位置的影响，同时通过修改分离诱导转捩关键参数，增加了模型对粗糙颗粒诱导强制转捩的敏感性，最后对耦合关系式也进行了适当的修改。为了验证修改后的模型对高超声速自然转捩和强制转捩的预测能力，对Ma7.4 Ames全尺寸模型和单个粗糙颗粒诱导Ma6的平板转捩进行了模拟。结果表明：与原始模型相比，修改后的模型的转捩位置被大大推迟，并且粗糙颗粒诱导转捩的作用被加强，与实验结果吻合良好。采用此模型对X-51A的20%缩比进气道模型在普渡大学Ma6静音风洞中的试验状态进行了模拟，模型不仅能够反映来流湍流度对转捩的影响，也能反映转捩带对转捩的促进作用。结果显示修改的转捩模型在高超声速复杂构型的转捩预测及研究中具有很好的应用潜力。Abstract: The correlation-based γ-Reθ transition model has been implemented into a large scale parallel compressible Navier-Stokes solver AHL3D. In order to simulate the effects of compressibility of the hypersonic flow, compressible modification has been added into this model. The constant parameter for the separation induced transition has been enhanced to improve the ability of the forced transition simulation. The correlation equations have been adjusted after all the modifications. In order to validate the modified models' ability to capture the transition location, a Ma=7.4 Ames all-body aircraft model for natural transition and a Ma=6 flat plate installed with three dimensional roughness elements for forced transition were simulated. The results show that compared to the original model, the modified model gives much later transition location and stronger effects of the roughness elements, which agree well with the experimental results. Finally, the modified model has been applied to the simulation of hypersonic natural and forced transition of the 20% scale X-51A fore body configuration in BAM6QT. The present model can simulate not only the effects of the free stream turbulence intensity but also the promotion of the transition position by the forced transition trips. The results show the good potential of the modified γ-Reθ transition model in transition prediction for complex configurations in hypersonic flows.
-
Keywords:
- transition model /
- boundary layer /
- hypersonic inlet /
- forced transition
-
0 引言
0.6m×0.6m连续式跨声速风洞(简称0.6m连续式风洞)是中国空气动力研究与发展中心高速空气动力研究所新建成的一座连续式风洞,主要用于对大型连续式风洞设计、建设和调试中的若干关键技术[1]进行预研和验证。
国际上，欧美等发达国家连续式风洞建设起步早，美国于1941年建成了4.7m的大型连续式高速风洞，英国于1942年建成了1.8m×2.4m的连续式跨声速风洞[2]。而国内由于受到经费、制造和加工水平限制以及发达国家的技术封锁，连续式风洞建设起步晚。西北工业大学于2003年建成了国内第一座连续式跨声速风洞。开展了轴流式压缩机的喘振边界线测试[3-6]，在连续式风洞设计与调试方面作了一定开创性的工作，但调试过程中也暴露出了一些问题和不足。目前国内在暂冲式跨声速风洞设计、建设和使用等方面技术成熟、经验丰富，已经建成了2m量级具有国际一流水平的大型跨超声速风洞(2.4m跨声速风洞和2m超声速风洞)，但同暂冲式风洞相比，连续式风洞不仅在驱动形式和运行原理上不同，而且在风洞的调试内容、调试方法和关键技术等方面也有诸多差异，因此在连续式风洞设计、建设及调试方面可借鉴的文献和经验很少。
为了了解和掌握轴流式压缩机的运行特点及安全运行边界以及实现压缩机转速和马赫数的精确控制，在风洞调试运行中开展压缩机防喘振控制和转速控制以及马赫数多变量控制关键技术研究，并给出具体的应用效果。
1 风洞介绍
0.6m连续式风洞结构轮廓图如图 1所示。试验段截面尺寸：0.6m×0.6m；风洞运行总压：p0=(0.15～2.5)×105Pa；总温：T0=(280～323)K；马赫数：Ma＝0.2～1.6；Re数范围：Rec=(0.1～2.25)×106(c=0.06m)。
该风洞配置了主、辅2套压缩机，其中主压缩机为静叶可调的AV90-3型三级轴流压缩机，辅压缩机为E71-3型离心压缩机，用于驻抽试验工况，与主压缩机配套使用辅助建立跨声速和低超声速流场。
2 控制方法研究
2.1 压缩机防喘振控制
目前，国内压缩机主要应用于大型钢铁、石油和化工等行业。该行业压缩机具有运行工况单一、转速变化范围小、工况范围窄和远离喘振点的特点。而对于连续式风洞这一特殊的管网系统，风洞流量大小由压缩机能提供的压比确定，风洞与压缩机二者形成闭环回路，整个系统的工作是一个相互耦合、作用的过程[7]，且压缩机具有运行工况点多，转速、压比和流量变化范围广，部分运行工况点靠近喘振边界线，同时由于压缩机转速、马赫数和模型姿态角等变量的剧烈变化，将严重影响整个管网系统的阻尼特性，极易诱发压缩机喘振，因此连续式风洞压缩机防喘振难度远远大于一般工业应用的压缩机。
2.1.1 喘振边界测定
在0.6m连续式风洞中，通过控制中心体二喉道流通面积，减小压缩机进气体积流量，对压缩机进行“逼喘”。在“逼喘”过程中分别在压缩机出/入口通过精密压力表实时测量压力波动，通过“压力波动法”[8]准确测量压缩机喘振边界。图 2给出了具体的试验结果。
2.1.2 防喘振控制
为了保证压缩机的安全运行，根据压缩机厂家的经验，需要设置合理防喘振线ε1=f1(Q)和防喘报警线ε2=f2(Q)。通常在实测喘振点的基础上保持压比不变，将体积流量增大3%~5%作为防喘振线，体积流量增大6%~10%作为防喘振报警线。而在连续式风洞中，由于压缩机使用经验少，运行工况复杂、多变，因此对喘振裕度的控制更加保守，结合风洞实际调试情况，并满足风洞试验运行工况要求，将体积流量分别增大6%和12%作为压缩机的防喘振线ε1=f1(Q)和防喘报警线ε2=f2(Q)。
图 3给出了该风洞轴流式压缩机实测喘振线、防喘振线、防喘振报警线以及各马赫数运行工况点的分布。
试验中，实时监控压缩机运行压比ε与对应体积流量下的喘振报警压比ε1和防喘振压比ε2。如果ε<ε1，机组运行安全；如果ε1≤ε<ε2，控制程序自动发出报警信息，但压缩机可以安全运行；如果ε≥ε2，触发防喘振控制，迅速打开防喘振阀或紧急停机，使压缩机远离喘振区。控制逻辑如图 4所示。
2.2 控制策略研究
2.2.1 压缩机转速控制
压缩机转速的精确控制是连续式风洞马赫数精确控制的基础。为达到风洞马赫数控制精度优于0.001~0.002的指标要求，风洞总体设计要求主压缩机的转速控制精度≤0.03%。
设计上，为了实现2台电机同步拖动的稳定运行和精确调速，研制了一套变频器调速系统。采用矢量控制技术，通过等效变换仿照直流电动机的控制方式，将异步电动机定子电流矢量分解为励磁电流和转矩电流进行控制，经电流、转速双闭环，达到控制异步电动机转矩和转速的目的，获得媲美直流调速的动态性能；由完全独立的2台变频器通过主、从机同步通讯，实时保持给定参数、控制参数、启停动作的一致性，实现转速同步、功率平衡。电流、转速双闭环矢量控制拓扑图如图 5所示。
调试中，为了实现矢量控制和同步控制功能，采取改变工况和开/闭环控制模式、优化转速采集方式、在线监测和比对运行数据等方法，通过变频器功能参数、控制参数以及电机参数的解耦，得出相关参数对矢量控制等效变换和变频器PID参数的影响关系，优化变频器参数，实现了同步、精确调速。
由于目前现有转速测量装置无法满足连续式风洞压缩机转速控制精度测量要求，为了考核调速精度，自主研制了一套转速测量装置[9]，基于编码器正交输出四倍频原理和M/T测速法原理[9-10]，达到了0.0034%的测速精度。该装置兼具测量精度高、测量周期短、数据实时显示和导出的特点，能够可靠实现编码器信号的复制、外接测量，解决了无法额外安装测速装置及安全风险问题。测速装置原理如图 6所示。
试验中选取5个转速[11-12]作为测试转速。待转速稳定后，在2min内采集转速不少于600次，由公式(1)[11]计算出转速控制精度。
(1) 测量结果如表 1所示，表明主压缩机在工作转速范围内转速控制精度满足≤0.03%的设计指标要求。
表 1 转速控制精度测试结果Table 1 Test result of the rotation control precision转速/(r·min-1) 最大转速/(r·min-1) 最小转速/(r·min-1) 控制精度/% 1500 1500.61 1499.63 0.0136 1800 1800.54 1799.8 0.0103 2400 2400.88 2399.17 0.0238 3000 3000.73 2999.51 0.0169 3600 3601.2 3599.12 0.0289 2.2.2 多变量控制策略研究
0.6m连续式风洞采用定总压、定马赫数的运行方式。为了满足设计要求，需要分别对风洞总压和马赫数进行精确控制。其中总压控制变量包括：压缩机转速、进/排气调压阀开度和中心体开度；马赫数控制变量包括：压缩机转速、总压、驻抽流量和中心体开度。由于各控制变量相互影响、相互耦合，极大地增加了控制难度。
2.2.2.1 总压控制策略研究
0.6m连续式风洞与2.4m暂冲式跨声速风洞相比，总压控制变量在进/排气调压阀控制变量的基础上，增加了一个压缩机转速控制变量，使得0.6m连续式风洞总压控制更加复杂。
压缩机转速对总压的影响机理是在增速过程中提高了压缩机的压比，增大了对风洞回路空气的压缩能力，而总压的闭环控制严重滞后于转速的变化，因此造成了压缩机增速过程中总压急剧增大，且转速变化越剧烈，对总压的影响越显著。图 7给出了常压工况下，压缩机转速对总压影响特性曲线。
稳转速状态下，压缩机转速只维持风洞回路气流的稳定流动，不会对总压造成二次影响，图 8给出了稳转速状态下，转速对总压的影响曲线。
![]()
图 8 稳转速状态下，转速与总压特性曲线Fig. 8 Rotating speed and stagnation pressure characteristic curves of steady state根据上述特性，为了消除连续式风洞压缩机转速对总压的影响，理想的办法是使压缩机保持稳态运行。即：固定各马赫数对应的压缩机转速，在该条件下，0.6m连续式风洞总压的控制可以简化为闭环控制进/排气调压阀开度，而2.4m暂冲式跨声速风洞总压控制即采用该控制策略[13]，具有成熟的使用经验。因此，0.6m连续式风洞总压控制策略为：固定进气调压阀和各马赫数对应的压缩机转速，闭环控制排气调压阀开度，实现总压的精确控制。
2.2.2.2 马赫数控制策略研究
由于0.6m连续式风洞采用定总压运行方式，因此，马赫数控制变量在原控制变量的基础上减少为压缩机转速、驻抽流量和中心体开度。为了达到精确控制马赫数的要求，首先要掌握各变量对马赫数的影响关系；其次根据影响关系，确定最佳的变量组合，实现马赫数精确控制。
(1) 控制变量对马赫数影响特性测试
(a) 转速与马赫数特性测试
图 9给出了声速喷管时，主压缩机转速与马赫数关系曲线。由图可知，Ma≤1时，马赫数与压缩机转速基本呈线性关系；Ma>1时，受到雍塞效应的影响，增加转速对提高马赫数的贡献较小。
(b)中心体开度与马赫数特性测试
图 10给出了不同主压缩机转速下中心体开度与马赫数关系曲线。由图可知，当Ma≤0.6时，中心体开度对马赫数的调节能力较弱，而Ma>0.6时，则对马赫数调节较为灵敏。
(c) 驻抽系统与马赫数控制特性测试
图 11给出了不同主/辅压缩机转速组合状态下，驻抽质量流量百分比与马赫数的关系曲线。结果表明，试验马赫数与驻抽流量百分比基本呈线性关系，只要驻抽流量一定，则马赫数与主/辅压缩机转速组合方式无关。
表 2给出了Ma=1.0不同主/辅压缩机转速组合时，总功率的对比。结果表明，相同马赫数下辅压缩机转速越低，总功率越小。主要是因为主压缩机为轴流式压缩机，流量大、压比小，而辅压缩机为离心式压缩机，流量小、压比高，从驻室内抽走相同质量的空气，辅压缩机需要耗费的功率更大。因此，驻抽试验状态时，宜采用主压缩机高转速、辅压缩机低转速的组合。
表 2 辅压缩机转速对能耗的影响Table 2 The effect of the assistant compressor’s rotation on energy consumptionMa 流量阀开度 主机转速/(r·min-1) 主机功率/kW 辅机转速/(r·min-1) 辅机功率/kW 总功率/kW 1 1 2765 2060 6150 505 2565 1 1 2729 1960 8571 1000 2960 (2) 马赫数控制策略研究
根据各控制变量对马赫数的影响特性曲线可知，压缩机转数是实现马赫数控制的主要变量。但为了实现压缩机转速对总压的解耦控制，在给定马赫数的条件下，只能通过中心体开度调节实现马赫的闭环控制。但当Ma>1.0时，由于壅塞效应的出现，需要通过驻抽系统对驻室静压的辅助抽吸来实现低超声速范围气流的膨胀。因此，Ma>1.0时，在此上述马赫控制的基础上，还需要增加驻抽系统，以实现Ma>1.0的马赫数控制。
在调试过程中发现Ma<0.6时，中心体对马赫数的调节能力较弱，调节周期较长;而采用压缩机转速对马赫数调节较快，且转速调节幅度较小，通过闭环控制排气调压阀能够满足总压的精确控制要求。因此在该马赫数范围，采用压缩机转速调节马赫数效果更好。
根据各控制变量对马赫数影响特性，并结合风洞试验调试情况，对马赫数采用分段控制策略。具体为： 0.2≤Ma≤0.6，采用主压缩机转速控制策略； 0.6<Ma≤1.0，采用固定马赫数对应的主压缩机转速，闭环控制中心体的控制策略；Ma>1.0时，采用固定各马赫数对应的主、辅压缩机转速，闭环控制中心体的控制策略。
3 调试结果
3.1 压缩机防喘振控制
在0.6m连续式风洞在调试和运行过程中，由于压缩机运行范围广，运行工况复杂、多变，多次出现压缩机运行工况点触碰防喘报警线和防喘振线的情况，防喘控制系统根据既定控制策略，自动实施了报警和打开防喘振阀的避喘操作，很好地保护了压缩机的安全。截止目前，压缩机已经累计安全运行长达1000余小时，充分证明该防喘振控制方法是安全和可靠的。
3.2 总压控制
根据0.6m连续式风洞总压控制策略，对于给定的马赫数，根据转速与马赫数的函数关系，计算出对应的压缩机转速。在转速调节过程，保持进气和排气调压阀开度，待压缩机进入稳态运行后，再投入总压闭环控制。图 12给出了具体试验结果。由图 12可知，采用该控制策略，成功实现了压缩机转速对总压的解耦控制，总压控制精度优于0.2%。
3.3 马赫数控制
在固定各马赫数对应压缩机转速，闭环控制中心体开度的控制策略的基础上，按照马赫数分段控制策略的方案，实现了0.6m连续式风洞马赫数的精确控制。图 13给出了调试结果。由图 13可见，采用该控制策略，能较好地实现马赫数的精确控制，马赫数控制精度优于0.002。
4 结论
(1) 采用压力波动法准确测量出了0.6m连续式风洞压缩机的喘振边界，设置了合理的报警线和防喘振线，确保了压缩机的安全运行，为掌握连续式风洞压缩机喘振边界测试积累了宝贵的经验。
(2) 采用矢量控制技术，通过等效变换，将异步电动机定子电流矢量分解为励磁电流和转矩电流进行控制，使得异步电动机调速的动态性能媲美直流电机，实现了压缩机转速的精确控制。
(3) 通过总压多变量控制策略研究，实现了压缩机转速对总压的解耦控制，总压控制精度优于0.2%。
(4) 通过马赫数多变量控制策略研究，在固定各马赫数对应压缩机转速，闭环控制中心体开度的控制策略的基础上，根据各变量对马赫数影响特性，采用分段控制方案，实现了马赫数的精度控制，控制精度优于0.002。
5 结束语
在0.6m连续式风洞中开展调试运行关键技术研究对积累大型连续式风洞调试经验和技术储备具有非常重要的指导意义。通过压缩机调试运行关键技术研究，了解并掌握了压缩机喘振边界测试方法、压缩机的防喘振控制以及安全运行监控等。其中“压力波动法”在国内压缩机喘振边界测试中是首次成功应用，解决了“噪声法”测量结果不准以及“振动法”测试风险大的难题；在马赫数控制策略研究中，从各控制变量对马赫数的影响特性出发，在诸多控制变量中实现了变量的解耦控制，找到了最佳变量组合实现了总压和马赫数的精确控制。
目前国内连续式风洞建设正处于起步阶段，由于人才、技术和调试经验的缺乏，还出现了其他一系列的问题。如：超声速流场的建立问题；跨声速工况下，中心体振动的问题；测力天平温度效应的问题；压缩机及风洞降噪的问题等等，都有待后续调试解决。
-
![]()
图 5 自然转捩热流分布(case1，修正后的模型)
Fig. 5 Heat flux distribution of natural transition (case1, modified model)
![]()
图 6 自然转捩热流分布(case2，修正后的模型)
Fig. 6 Heat flux distribution of natural transition (case2, modified model)
![]()
图 7 强制转捩热流分布(case3，修正后的模型)
Fig. 7 Heat flux distribution of forced transition (case3, modified model)
![]()
图 8 多套网格计算结果(case2，修正后的模型)
Fig. 8 Heat flux distribution of three meshes (case2, modified model)
![]()
图 12 迎风面的St数分布和摩擦力线
Fig. 12 Stanton number distribution and friction force lines of the windward
![]()
图 15 红外热试验和计算得到的St数分布(圆柱形粗糙颗粒诱导转捩)
Fig. 15 Infra-red visualization and calculated Stanton number distribution for cylinder roughness elements
![]()
图 16 红外热试验和计算得到的St数分布(钻石形粗糙颗粒诱导转捩)
Fig. 16 Infra-red visualization and calculated Stanton number distribution for diamond roughness elements
![]()
图 17 尾迹区和非尾迹区的St数对比
Fig. 17 Comparison of St number in and out of wake region for cylinder and diamond roughness elements
![]()
图 18 粗糙颗粒下游的流向涡发展情况
Fig. 18 Development of stream wise vortex downstream of the roughness elements
![]()
图 19 20%缩比X-51A前体构型示意图
Fig. 19 Windward side of 20% scale X-51A forebody configuration
![]()
图 20 迎风面测量得到的壁面温度和计算得到的摩阻系数(case5)
Fig. 20 Measured surface temperature and calculated skin friction for windward surface (case5)
![]()
图 21 迎风面测量得到的壁面温度和计算得到的摩阻系数(case6)
Fig. 21 Measured surface temperature and calculated skin friction for windward surface (case6)
![]()
图 23 中心线上测量得到的壁面温度和计算得到的摩阻系数(case4, case5)
Fig. 23 Measured surface temperature and calculated skin friction of the center line (case4, case5)
![]()
图 24 中心线上测量得到的壁面温度和计算得到的摩阻系数(case6)
Fig. 24 Measured surface temperature and calculated skin friction of the center line (case6)
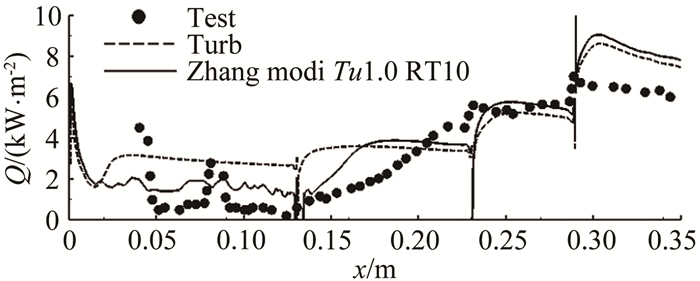
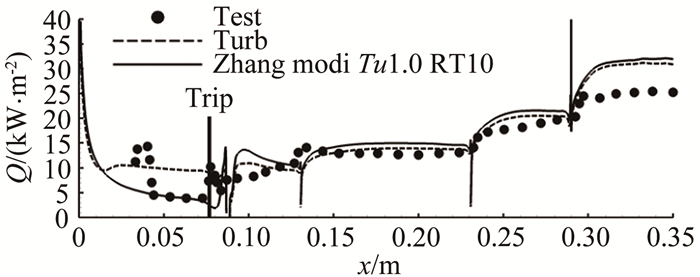
表 1 二维计算时进气道来流条件
Table 1 Free stream condition for 2-D inlet simulation
Case Ma 总压/
MPa总温/
K迎角/
(°)Re/
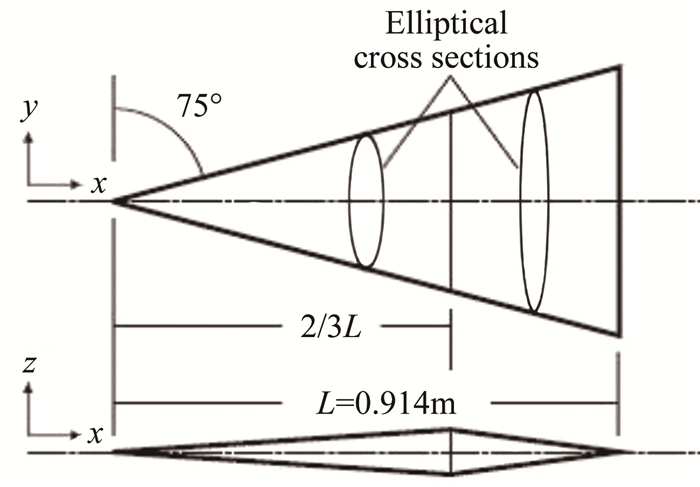
(107·m-1)转捩类型 1 5.96 2.00 473.2 1.0 1.82 自然 2 4.97 1.01 357.7 -0.6 2.21 自然 3 5.96 2.00 473.2 1.0 1.82 强制 
下载: 导出CSV
表 2 全尺寸升力体模型风洞试验来流条件
Table 2 Test conditions for the all-body model
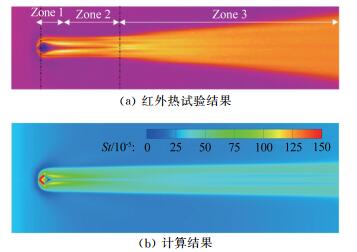
Ma Re/m-1 总温/K 静温/K 壁面温度/K 迎角/(°) 7.4 15×106 722 62 300 15
下载: 导出CSV
表 3 20%缩比X-51A构型的试验条件
Table 3 Test conditions for the 20% scaled X-51A forebody configuration
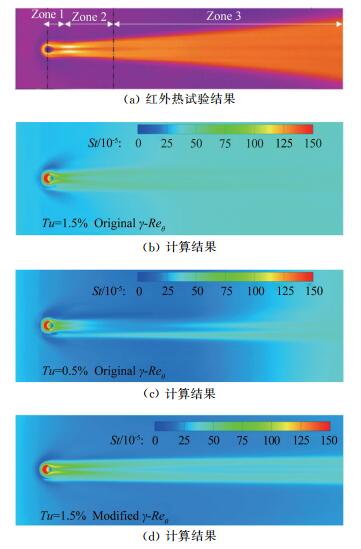
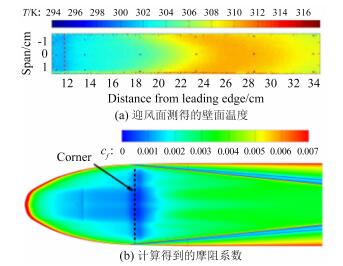
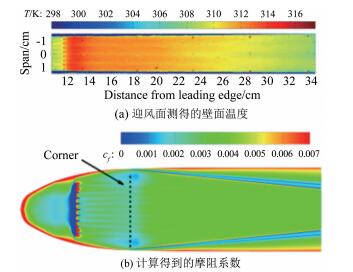
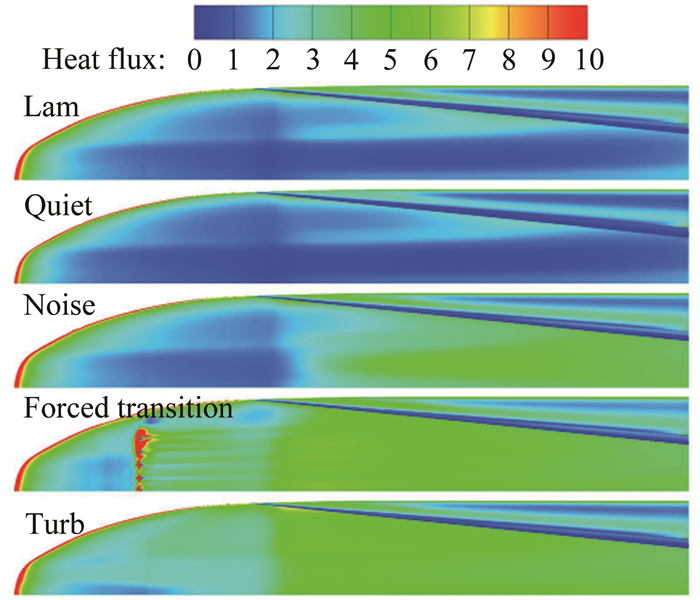
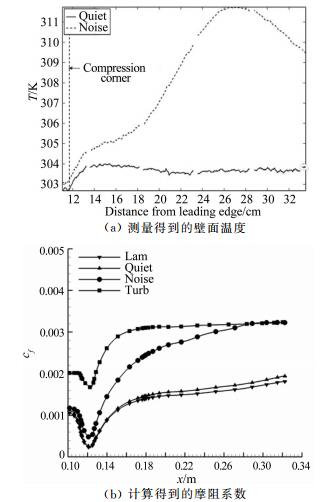
Case Ma Re/m-1 总压/kPa 总温/K 来流湍流度 转捩类型 4 6.00 6.59×106 586 418 0.05% 自然 5 5.80 7.40×106 621 424 3.00% 自然 6 5.78 7.35×106 614 424 3.00% 强制
下载: 导出CSV
-
[1] Mayer C S J, Terzi D A V, Fasel H F. DNS of complete transition to turbulence via oblique breakdown at Mach3[R]. AIAA-2008-4398, 2008.
[2] Ducros F, Comte P, Lesieur M. Large-eddy simulation of transition to turbulence in a boundary layer developing spatially over a flat plate[J]. Journal of Fluid Mechanics, 1996, 326:1-36. DOI: 10.1017/S0022112096008221
[3] Mack L M. Boundary layer linear stability theory[R]. AGARD Report No.709, 1984.
[4] Kocian T S, Moyes T, Mullen C D, et al. PSE and spatial biglobal instability analysis of HIFiRE-5 geometry[R]. AIAA-2016-3346, 2016.
[5] Scott S, Nowak R J, Horvath T J. Boundary layer control for hypersonic airbreathing vehicles[R]. AIAA-2004-2246, 2004.
[6] Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables-part1: model formulation[R]. GT-2004-53452, 2004.
[7] Langtry R B. A correlation-based transition model using local variables for unstructured parallelized CFD codes[D]. Stuttgart: University of Stuttgart, 2006.
[8] Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12):2894-2906. DOI: 10.2514/1.42362
[9] Watanabe Y, Misaka M, Obayashi S, et al. Application of crossflow transition criteria to local correlation-based transition model[R]. AIAA-2009-1145, 2009.
[10] Seyfert C, Krumbein A. Correlation-based transition transport modeling for three-dimensional aerodynamic configurations[R]. AIAA-2012-0448, 2012.
[11] Grabe C, Krumbein K. Correlation-based transition transport modeling for three-dimensional aerodynamic configurations[J]. Journal of Aircraft, 2013, 50(5):1533-1539. DOI: 10.2514/1.C032063
[12] Langel C M, Chow R, Dam P V. A computational approach to simulating the effects of realistic surface roughness on boundary layer transition[R]. AIAA-2014-0234, 2014.
[13] Krause M, Behr M, Ballmann J. Modeling of transition effects in hypersonic intake flows using a correlation-based intermittency model[R]. AIAA-2008-2598, 2008.
[14] Zhang X D, Gao Z H. A numerical research on a compressibility-correlated Langtry's transition model for double wedge boundary layer flows[J]. Chinese Journal of Aeronautics, 2011, 24(3):249-257. DOI: 10.1016/S1000-9361(11)60030-7
[15] Cheng G, Nichols R, Neroorkar K, et al. Validation and assessment of turbulence transition models[R]. AIAA-2009-1141, 2009.
[16] Bensassi K, Lani A, Patrick. Rambaud P. Numerical investigations of local correlation-based transition model in hypersonic flows[R]. AIAA-2012-3151, 2012.
[17] 赵慧勇.超燃冲压整体发动机并行数值研究[D].绵阳: 中国空气动力研究与发展中心, 2005. Zhao H Y. Massively parallel computation on scramjet combustor[D]. Mianyang: China Aerodynamics Research and Development Center, 2005.
[18] Le J L, Yang S H, Liu W X, et al. Massively parallel simulations of kerosene-fueled scramjet[R]. AIAA-2005-3318, 2005.
[19] 尚庆, 陈林, 李雪, 等.高超声速钝锥双楔绕流流动转捩与分离流动的壁温影响[J].航空学报, 2014, 35(11):2958-2969. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201411007.htm Shang Q, Chen L, Li X, et al. Wall temperature effect on transition flow and separated flow in hypersonic flow around a blunt double wedge[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11):2958-2969. http://www.cnki.com.cn/Article/CJFDTotal-HKXB201411007.htm
[20] Reshotko E. Is Reθ/Me a meaningful transition criterion?[J]. AIAA Journal, 2007, 45(7):1441-1443. DOI: 10.2514/1.29952
[21] 赵慧勇, 周瑜, 倪鸿礼.高超声速进气道边界层转捩试验[J].实验流体力学, 2012, 26(1):1-6 DOI: 10.3969/j.issn.1672-9897.2012.01.001 Zhao H Y, Zhou Y, Ni H L, et al. Test of forced boundary-layer transition on hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1):1-6. DOI: 10.3969/j.issn.1672-9897.2012.01.001
[22] 易淼荣, 赵慧勇, 乐嘉陵.强制转捩对高超声速进气道性能影响[J].航空动力学报, 2016, 31(8):1830-1837. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201608005 Yi M R, Zhao H Y, Le J L. Effect of forced-transition on performance of hypersonic inlet[J]. Journal of Aerospace Power, 2016, 31(8):1830-1837. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201608005
[23] Forsythe J R, Hoffmann K, Suzen Y. Investigation of modified Menter's two-equation turbulence models for supersonic applications[R]. AIAA-99-0873, 1999.
[24] Lockman W K, Lawrence S L, Cleary J W. Flow over an all-body hypersonic aircraft-experiment and computation[J]. Journal of Spacecraft and Rockets, 1992, 29(1):7-15. DOI: 10.2514/3.26308
[25] Tirtey S C, Chazot O, Walpot L. Characterization of hypersonic roughness-induced boundary-layer transition[J]. Experiments in Fluids, 2011, 50(2):407-418. DOI: 10.1007/s00348-010-0939-4
[26] Tirtey S C, Walpot L, Chazot O. Characterization of hypersonic roughness induced transition for the EXPERT flight experiment[R]. AIAA-2009-7215, 2009.
[27] Wang L, Xiao L, Fu S. A modular RANS approach for modeling hypersonic flow transition on a scramjet-forebody configuration[J]. Aerospace Science and Technology, 2016, 56:112-124. DOI: 10.1016/j.ast.2016.07.004
[28] Wang L, Fu S. Development of anintermittency equation for the modeling of the supersonic/hypersonic boundary layer flow transition[J]. Flow Turbulence and Combust, 2011, 87(1):165-187. DOI: 10.1007/s10494-011-9336-1
[29] Orlik E, Fedioun I, Davidenko D. Boundary-layer transition on a hypersonic forebody:experiments and calculations[J]. Journal of Spacecraft and Rockets, 2011, 48(4):545-555. DOI: 10.2514/1.51570
[30] Borg M P. Entitled laminar instability and transition on the X-51A[D]. West Lafayette: Purdue University, 2009.
-
期刊类型引用(1)
1. 唐志共，袁先旭，钱炜祺，肖涵山，毕林，王文正. 高速空气动力学三大手段数据融合研究进展. 空气动力学学报. 2023(08): 44-58 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 276
- HTML全文浏览量: 196
- PDF下载量: 26
- 被引次数: 1
