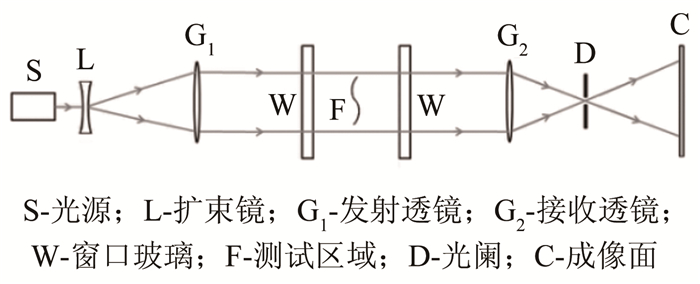
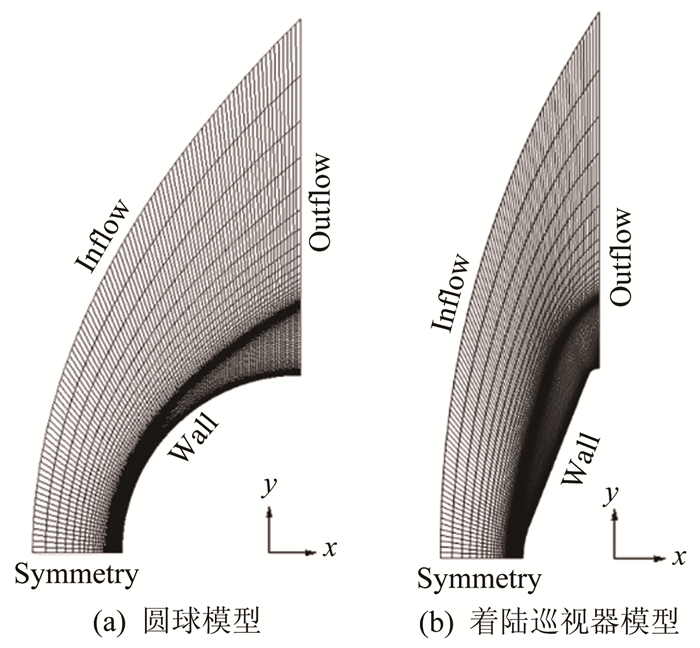
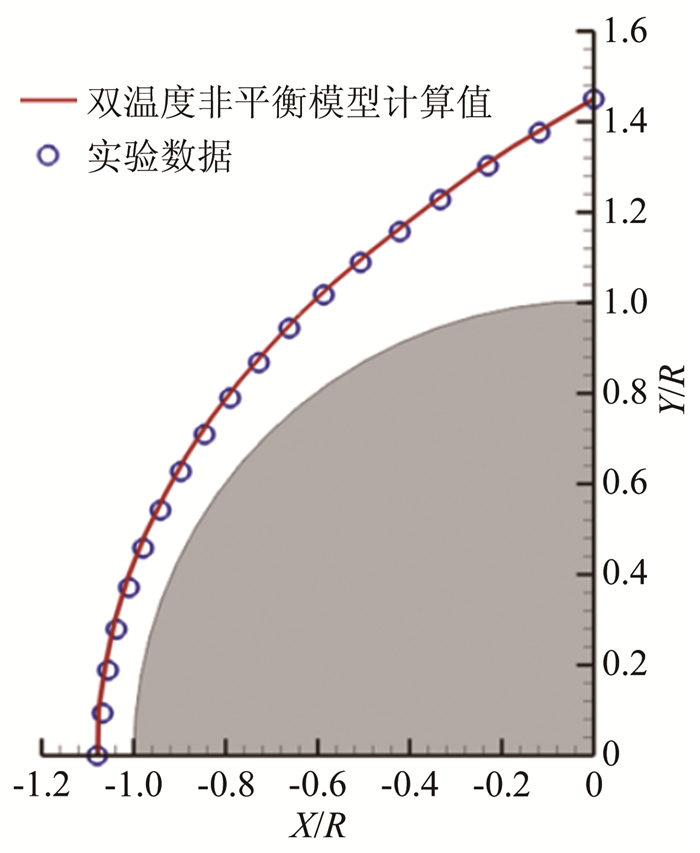
Ballistic range measurement and numerical calculation of shock standoff distances in CO2
-
摘要: 在中国空气动力研究与发展中心超高速所超高速弹道靶进行了CO2条件下圆球和火星着陆巡视器模型的激波脱体距离测量实验,为数值模拟提供验证依据。实验模型为φ10mm圆球和头部半径12.5mm的着陆巡视器模型。圆球模型的飞行速度为2.122~4.220km/s,靶室压力为2.42~12.30kPa;着陆巡视器模型的飞行速度为2.802km/s,对应靶室压力为1.836kPa。实验数据与采用双温度非平衡模型计算的结果进行了对比。得到以下结论:采用双温度非平衡模型能够较准确地再现模型头部激波脱体距离;根据计算结果推测绕模型流动主要为非平衡流动;需补充更高模型飞行速度(>5km/s)的实验数据,验证CO2中更高流速状态下双温度非平衡模型的适用性与准确性,并进一步研究多温度模型和不同化学反应动力模型对CO2下非平衡流数值计算准确性的影响。Abstract: Measurement of shock standoff distances over spheres and the Mars entry vehicle model in CO2 has been conducted in the hypervelocity ballistic range of Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center. Test models were spheres with the diameter of 10mm and entry vehicle models with the nose radius of 12.5mm. For spheres, the flight velocities were between 2.122 and 4.220km/s with ambient pressures between 2.42 and 12.3kPa. For the entry vehicle model, the flight velocity was 2.802km/s with the ambient pressure of 1.836kPa. Comparison was made between the test data and calculated results using the two-temperature nonequilibrium model. Under present test conditions, the two-temperature nonequilibrium model can basically reproduce the shock standoff distances over the test models. The flow over the test models is speculated to be mainly nonequilibrium. More test data with higher flight velocities (>5km/s) are needed for the validation of the two-temperature nonequilibrium model in CO2 with higher freestream velocity. The influence of multi-temperature models and different chemical reaction models on the accuracy of the numerical simulation for the nonequlilbirum flow in CO2 can be further studied.
-
Keywords:
- nonequilibrium /
- shock standoff distance /
- ballistic range experiment /
- two-temperature model /
- CO2
-
0 引言
目前,要求地面试验设备完全模拟高超声速飞行环境是非常困难的,在一个试验设备上进行所有环境的模拟试验更是不可能的。因此,需要研制多种试验设备,以满足高超声速试验需求[1-5]。
常规高超声速风洞主要模拟参数是马赫数和雷诺数[6],其他一些参数则主要通过高焓试验设备来模拟[7-8]。
在高超声速风洞运行中,气源不仅要维持风洞所必须达到的压力比,还需要满足雷诺数模拟的要求。一般来说,风洞的总压要足够高。如果风洞连续工作,高的压力比和高总压将使风洞消耗很大的动力,因而高超声速风洞多为暂冲式。
暂冲式常规高超声速风洞的运行方式是:气罐中的压缩空气经过加热系统达到所需温度,然后通过型面喷管,在试验段形成所需的高超声速流场,最后经由超声速扩散段升压后进入引射排气系统,排入大气,或经过冷却器进入真空系统,由真空泵系统排入大气。常规高超声速风洞一般加热温度在800K以下,主要是为了防止气流冷凝,不能真实模拟实际总温(马赫数6时达到1800K),因此,开展发动机及飞行器一体化带动力试验还需要满足总温要求的高焓设备。
燃烧加热风洞是目前高超声速飞行器地面模拟试验尤其是带动力试验的主要设备。在过去的十几年间,中国空气动力研究与发展中心研制了不同尺度的脉冲燃烧风洞,探索了一体化飞行器设计、计算与试验技术[7-9]。在此基础上,发展了基于脉冲燃烧风洞的大尺度飞行器带动力一体化试验技术[10-11],提出了一种基于一体化试验直接测力结果的飞行器和发动机性能评估方法。
由于采用燃烧加热方式,无论是采用氢燃料还是碳氢燃料,都会产生水蒸气(H2O)、二氧化碳(CO2)等燃烧产物,即形成所谓“污染”。污染组分将造成风洞试验气体物理化学属性与真实空气存在一定差异,导致地面试验难以完全模拟真实飞行状态下的所有来流参数,且给地面试验结果向真实飞行状态的外推带来不确定性。为了尽可能降低这种不确定性,地面试验一般需要慎重考虑试验来流与模拟对象环境之间的参数匹配问题:即通过有选择地调整污染来流的某些状态参数,使之逼近对应的真实飞行环境,同时放弃一些无法兼顾的非关键参数,以尽可能达到飞行器气动与推进性能的可靠模拟。
目前主要有两种模拟方式:对于气动力试验,一般采用静温、静压、马赫数模拟;对于发动机性能试验,也可以采用总焓、动压、马赫数模拟。
中国科技大学杨基明、罗喜胜等[12-13]通过典型升力体飞行器的试验和计算研究,证明污染组分使得斜激波波后参数相对纯净空气有一定变化,从而造成模型表面压力及模型的气动力有一定变化,但变化量较小。相对于纯净空气来流,污染空气来流时发动机推力、单位推力、比冲均有所下降。脉冲燃烧风洞采用氢氧燃烧加热,污染空气来流时推力性能下降相对较小,与纯净空气来流时较为接近。
西北工业大学宋文艳等[14]研究了H2O/CO2污染煤油燃料对超声速燃烧室的影响,认为污染对点火和超声速燃烧具有一定的抑制作用,污染组分的存在会导致燃烧室模态转换点发生变化。
谭宇等[15]在酒精燃烧和氢气燃烧两种加热方式的风洞设备上开展了匹配方案对超燃冲压发动机性能影响的试验研究,比较了两种目前较常用的气流参数匹配方案,结果表明:对于采用氢气燃烧加热方式的风洞设备,总焓动压马赫数(h0QM)匹配比静温静压马赫数(TPM)匹配能够获得更高的壁面静压和推力收益;对于采用酒精燃烧加热方式的风洞设备,两种匹配方案表现相当。
壁温比通常定义为模型壁面温度与恢复温度的比值。常规高超声速风洞来流温度较低,气流壁面恢复温度与壁面温度相差不大,接近于绝热状态;而燃烧加热脉冲风洞来流温度较高,风洞试验时间很短(300~600ms),壁面温度基本保持常温,接近于等温状态,气流壁面恢复温度与试验模型表面温差较大,气流对壁面的加热效应明显。壁面温度条件会影响到高超声速边界层内的流动参数,进而影响到流场的波系结构和气动性能。壁温降低引起摩擦系数的增加和边界层厚度减小,使得激波边界层作用区域变小;同时,冷壁使得边界层内亚声速部分声速较低,马赫数更高。
为了评估真实飞行条件下的飞行器气动性能,需重点考虑壁温对燃烧加热脉冲风洞试验结果的影响。
本文采用不通气标模,在常规高超声速风洞以及两个不同尺度(Φ2.4m和Φ600mm)的脉冲燃烧风洞中开展对比测力试验,结合数值计算,研究脉冲燃烧风洞水凝结、雷诺数及壁温比对模型气动性能的影响规律。
1 试验模型
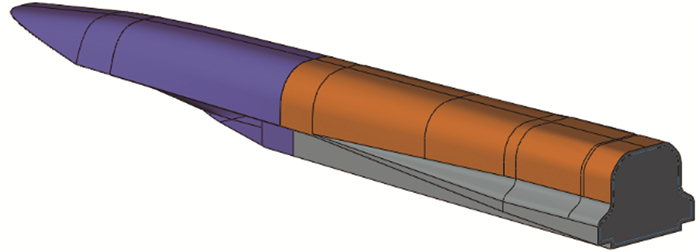
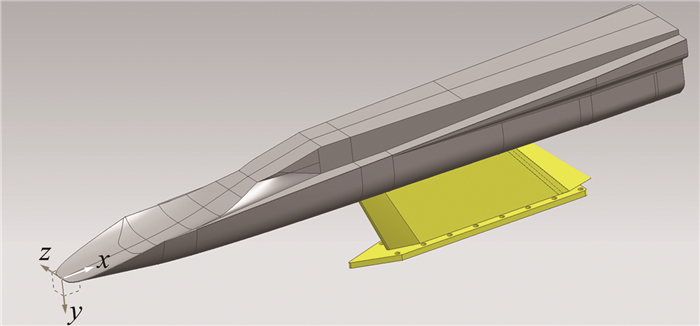
试验模型采用不通气标模。对应Φ2.4m脉冲燃烧风洞,试验模型为大不通气标模,采用背部支撑,如图 1所示;对应常规高超声速风洞和Φ600mm脉冲燃烧风洞,试验模型为1/5缩比的小不通气标模,采用尾部支撑,如图 2所示。
2 脉冲燃烧风洞水凝结影响研究
为了获得水凝结对脉冲燃烧风洞试验数据的影响,采用小不通气标模,在Φ600mm脉冲燃烧风洞开展不同总温条件下的对比试验研究,分析测力结果。
2.1 对比试验参数
对Φ600mm脉冲燃烧风洞喷管进行了试验配套改造,在来流总温、组分不同的条件下,保持风洞出口马赫数一致。以现有的Ma6喷管为基础(总温1500K),设计制造总温为1200和1800K的喉道段,喷管出口马赫数与现有喷管一致。表 1为不通气高超标模试验参数(p0、T0分别为总压、总温,p、T分别为静压、静温)。
表 1 不同总温高超标模试验参数Table 1 Flow parameters of different T0 testsMa p0/MPa T0/K p/Pa T/K Re 6.0 4.5 1200 2368 162 7.08×106 6.0 5.1 1500 2398 210 4.98×106 6.0 5.8 1800 2374 263 3.61×106 2.2 试验结果
图 3、4给出了不通气高超标模的轴向力系数CA、法向力系数CN随迎角α变化的试验结果曲线。
试验表明:在总温1200~1800K试验状态下,最大轴向力系数差别为5.4%,说明水凝结对不通气高超标模的轴向力影响很小,约为5%左右。在-2°迎角时,总温1200K(有水凝结)试验状态的法向力系数较总温1500K减小了约40%;在0°~6°迎角下,法向力系数减小12%~5%,说明随着迎角的增加,模型下表面的凝结水蒸发,导致水凝结对法向力的影响减小。在-2°迎角时,总温1800K试验状态的法向力系数较总温1500K增加了约30%,说明总温1500K、-2°迎角状态在模型的下表面也发生了水凝结,导致模型下表面流场压力升高,法向力系数减小;而在其他迎角状态,总温1500K时并没有发生水凝结现象,因此法向力系数差别较小。
3 脉冲燃烧风洞雷诺数影响研究
3.1 对比试验参数
为了获得雷诺数对试验结果的影响,用不同尺度的不通气标模在Φ2.4m脉冲燃烧风洞和Φ600mm脉冲燃烧风洞进行对比试验,试验参数见表 2(CHIF:脉冲燃烧风洞)。
表 2 试验参数Table 2 Test parametersFacility Ma T0/K p0/MPa Φ2.4m CHIF 6 1575 4.76 Φ600mm CHIF 6 1500 4.61 3.2 试验和计算结果
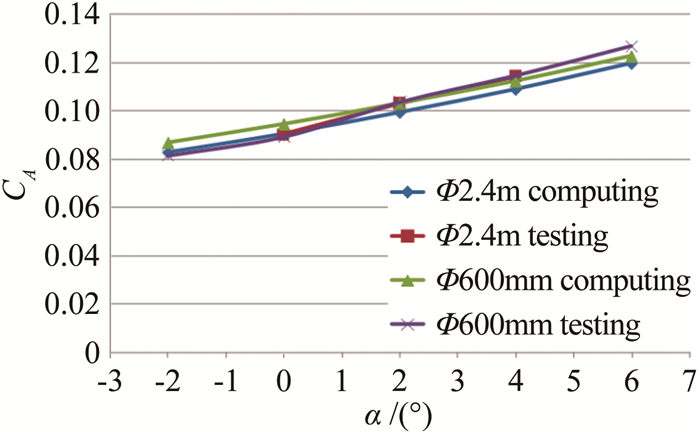
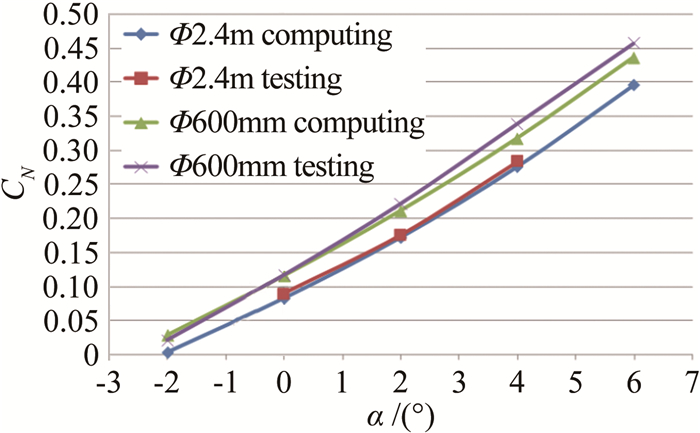
图 5和6给出了大、小不通气标模在两个脉冲燃烧风洞的轴向力系数CA、法向力系数CN试验结果,同时也给出了两个模型按照对应风洞来流条件计算获得的气动力系数结果。
计算结果表明:模型尺度对不通气标模的轴向力有一定影响,小不通气标模的轴向力略大于大不通气标模,相差约2%~5%。由于两个脉冲燃烧风洞模拟条件基本相同,试验时间也接近,因此这个差异可以解释为模型尺度(雷诺数)造成的:小不通气标模的雷诺数小于大不通气标模,因此轴向力略大。试验并未能够反映出雷诺数的影响,这可能是由于两个模型支撑方式不同以及试验测量误差掩盖了差异。
两个模型的法向力结果不一致,主要是由于支撑方式不同造成的。前期研究表明,腹部支撑对轴向力影响不大,但对法向力影响显著。
计算与试验结果符合较好,使计算和试验得到了相互验证。
4 脉冲燃烧风洞壁温比影响研究
采用小不通气标模,通过Φ600mm脉冲燃烧风洞及常规高超声速风洞的试验对比,结合数值计算,研究壁温比对脉冲燃烧风洞试验结果的影响。
4.1 对比试验参数
Φ600mm脉冲燃烧风洞与Φ1m常规高超声速风洞的试验流场存在总温、雷诺数、壁温比等方面的差异。假设壁温300K,风洞流场参数对比如表 3所示(HWT:常规高超声速风洞;Tratio为壁温比)。
表 3 Φ1m常规高超声速风洞与Φ600mm脉冲燃烧风洞流场参数Table 3 Test parameters of Φ1m hypersonic wind tunnel and Φ600mm combustion heated impulse facilityFacility Ma p0/MPa T0/K γ Re Tratio Φ1m HWT 6.0 3.00 500 1.40 2.62×107 5.17 Φ600mm CHIF 6.0 4.65 1560 1.36 4.10×106 1.49 4.2 试验和计算结果
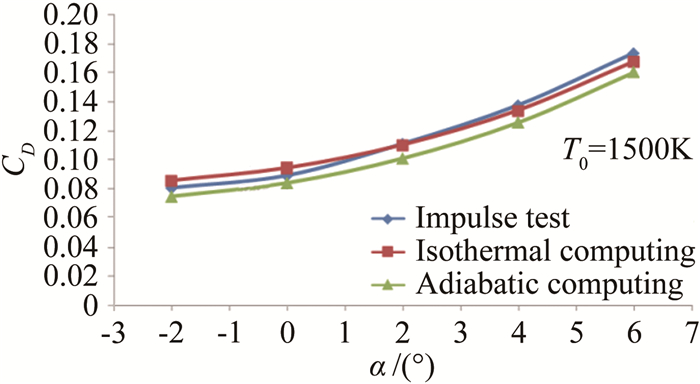
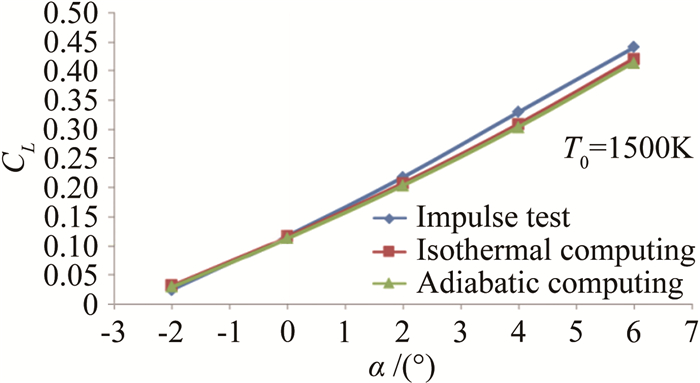
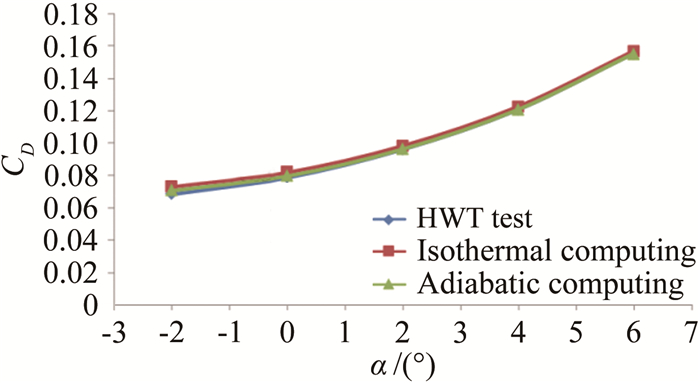
脉冲燃烧风洞试验与计算结果表明:采用等温壁300K条件计算获得的阻力系数与试验数据比较接近,误差在6%以内;绝热壁计算阻力系数较等温壁300K计算小5%(迎角6°)~15%(迎角-2°);不同壁温条件对升力系数的计算结果影响不大,与试验结果的误差分别在6%和8%以内;采用等温壁300K条件计算获得的结果与试验基本一致。图 7和8给出了脉冲燃烧风洞试验和计算的阻力系数CD及升力系数CL的对比曲线。
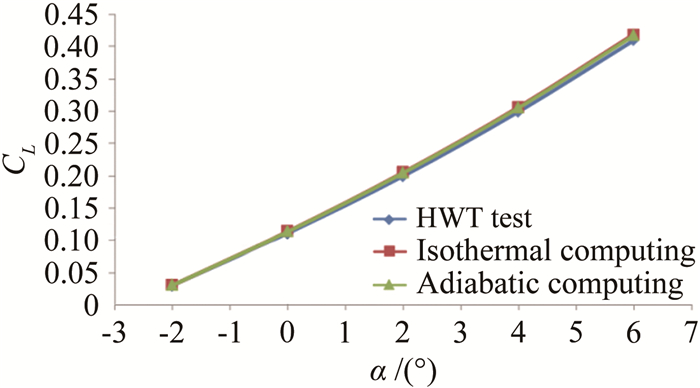
常规高超声速风洞试验和计算结果表明:不同壁温条件对计算结果影响不大,计算结果与试验符合较好,阻力误差在4%以内,升力误差在3%以内。图 9和10给出了相应的阻力系数和升力系数比较曲线。
通过试验验证,表明数值计算具有较高的可信度。为了进一步分析规律,采用数值计算分析了脉冲燃烧风洞与常规高超声速风洞阻力系数的数据相关性,如图 11所示。
(1) 脉冲燃烧风洞等温壁计算得到的阻力系数比常规高超声速风洞大7%(迎角6°)~17%(迎角-2°),迎角越小,差异越大。这个差异由多方面因素导致,主要有雷诺数、比热比、壁温比等。
(2) 针对同一个模型,分别采用脉冲燃烧风洞和常规高超声速风洞的模拟参数计算(壁面都取绝热壁条件),此时得到的结果差异应该排除了壁温比的影响,而反映了两个风洞模拟条件(如雷诺数、比热比)不同引起的变化量,计算获得的这一部分的影响量约为3%(迎角6°)~6%(迎角-2°)。
(3) 除去两个风洞模拟条件(如雷诺数、比热比)不同引起的阻力变化量,可得到壁温比的影响量约为4%(迎角6°)~12%(迎角-2°),迎角越小,差异越大。
5 结论
通过脉冲燃烧风洞与常规高超声速风洞不通气高超标模对比试验和计算,得到如下结论:
(1) 脉冲燃烧风洞获得的气动力系数变化规律与常规高超声速风洞一致;
(2) 雷诺数、壁温比对阻力系数均有影响,其中壁温比影响显著,脉冲燃烧风洞获得的阻力系数明显大于常规高超声速风洞;
(3) 水凝结对不通气高超标模的轴向力影响较小,对法向力影响较大,且不同迎角状态影响量不同。
-
表 1 模型头部激波脱体距离测量数据和对应实验状态
Table 1 Shock standoff distances at the spheres' nose under various test conditions
编号 模型直径
D/mm飞行速度
V/(km·s-1)靶室压力
p/kPa靶室温度
T/K马赫数
Ma雷诺数
Re*双尺度参数
ρR/(kg·m-2)无量纲激波脱体距离
δ/R测量误差
E/RC10-1 10 2.122 12.300 292.1 7.6 3.2×105 1.1×10-3 0.0795 ±3.89% C10-2 10 2.845 7.425 293.2 10.2 2.6×105 6.7×10-4 0.0705 ±4.37% C10-3 10 4.220 2.420 293.7 15.1 1.2×105 2.2×10-4 0.0618 ±4.88% *雷诺数以直径10mm计。 表 2 着陆巡视器头部激波脱体距离测量数据和对应实验状态
Table 2 Shock standoff distances at the entry vehicle models' nose under various test conditions
编号 头部半径
Rn/mm飞行速度
V/(km·s-1)靶室压力
p/kPa靶室温度
T/K马赫数
Ma雷诺数
Re*双尺度参数
ρRn/(kg·m-2)无量纲激波脱体距离
δ/Rn测量误差
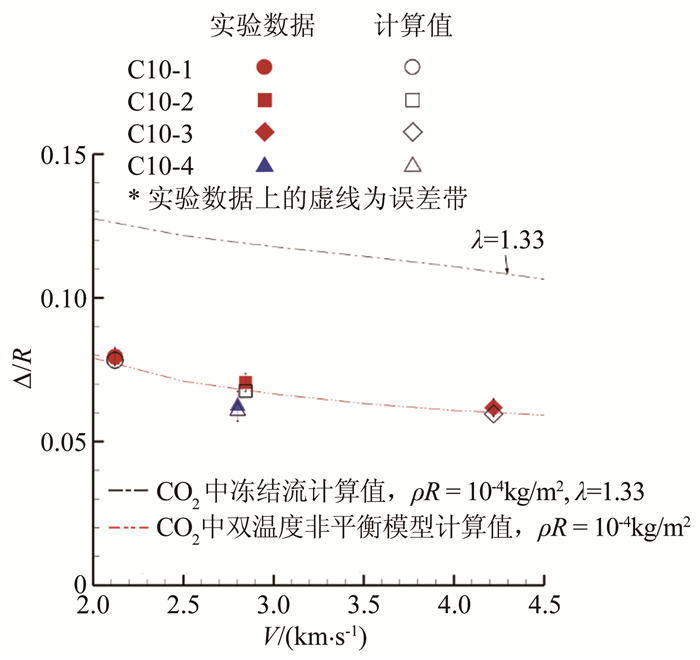
E/RnC10-4 12.5 2.802 1.836 294.7 10.0 1.6×105 4.1×10-4 0.0623 ±8.34% *雷诺数以大底直径25mm计。 表 3 模型头部激波脱体距离实验数据与计算结果对比
Table 3 Comparison between tested and the calculated shock standoff distances at the models' nose
编号 激波脱体距离实验值δ/R(δ/Rn) 测量误差E/R 激波脱体距离计算值δ/R(δ/Rn) 计算结果相对实验数据偏差 C10-1 0.0795 ±3.89% 0.0783 -1.51% C10-2 0.0705 ±4.37% 0.0676 -4.11% C10-3 0.0618 ±4.88% 0.0596 -3.56% C10-4 0.0623 ±8.34% 0.0607 -2.57% -
[1] 韩鸿硕, 陈杰. 21世纪国外深空探测发展计划及进展[J].航天器工程, 2008, 17(3):1-22. http://d.old.wanfangdata.com.cn/Periodical/htqgc200803001 Han H S, Chen J. 21st century foreign deep space exploration development plans and their progresses[J]. Spacecraft Engineering, 2008, 17(3):1-22. http://d.old.wanfangdata.com.cn/Periodical/htqgc200803001
[2] 廖东骏, 柳森, 简和祥, 等.高超声速球头激波脱体距离研究综述[J].实验流体力学, 2015, 29(6):1-7. http://www.syltlx.com/CN/abstract/abstract10882.shtml Liao D J, Liu S, Jian H X, et al. A review of hypersonic sphere shock standoff distance research[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6):1-7. http://www.syltlx.com/CN/abstract/abstract10882.shtml
[3] Park C. The limits of two-temperature model[R]. AIAA-2010-911, 2010.
[4] Nonaka S, Mizuno H, Takayama K, et al. Measurement of shock standoff distance for sphere in ballistic range[J]. Journal of Thermophysics and Heat Transfer, 2000, 14(2):225-229. DOI: 10.2514/2.6512
[5] 柳军, 乐嘉陵, 杨辉.高超声速圆球模型飞行流场的数值模拟和实验验证[J].流体力学实验与测量, 2002, 16(1):67-73. DOI: 10.3969/j.issn.1672-9897.2002.01.011 Liu J, Le J L, Yang H. Numerical simulation of hypersonic flowfield around sphere model and experimental verification[J]. Experiments and Measurements in Fluid Mechanic, 2002, 16(1):67-79. DOI: 10.3969/j.issn.1672-9897.2002.01.011
[6] Zander F, Gollan R J, Jacobs P A, et al. Hypervelocity shock standoff on spheres in air[J]. Shock Wave, 2014, 14:171-178. DOI: 10.1007/s00193-013-0488-x
[7] 史建魁, 张仲谋, 刘振兴, 等.火星环境探测结果分析[J].地球物理学进展, 1997, 12(4):98-108. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700941240 Shi J K, Zhang Z M, Liu Z X, et al. An analysis of results of the Martian environment exploration[J]. Progress in Geophysics, 1997, 12(4):98-108. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700941240
[8] MacClean M, Holden M. Catalytic effects on heat transfer measurements for aerothermal studies with CO2[R]. AIAA-2006-0182, 2006. http://www.researchgate.net/publication/268564464_catalytic_effects_on_heat_transfer_measurements_for_aerothermal_studies_with_co2
[9] Doraiswamy S, Kelley D, Candler V G. Vibrational modeling of CO2 in high-enthalpy nozzle Flow[J]. Journal of thermophysics and heat transfer, 2010, 24(1):9-17. DOI: 10.2514/1.43280
[10] MacLean M, Dufrene A, Holden M. Spherical capsule heating in high enthalpy carbon dioxide in LENS-XX expansion tunnel[R]. AIAA-2013-0906, 2013. http://www.researchgate.net/publication/268468442_Spherical_Capsule_Heating_in_High_Enthalpy_Carbon_Dioxide_in_LENS-XX_Expansion_Tunnel
[11] Sharma S P, Park C. Survey of simulation and diagnostic techniques for hypersonic nonequilibrium flows[J]. Journal of Thermophysics and Heat Transfer, 1990, 4(2):129-142. DOI: 10.2514/3.155
[12] 柳森, 王宗浩, 谢爱民, 等.高超声速锥柱裙模型边界层转捩的弹道靶实验[J].实验流体力学, 2013, 27(6):26-31. DOI: 10.3969/j.issn.1672-9897.2013.06.005 Liu S, Wang Z H, Xie A M, et al. Ballistic range experiments of hypersonic boundary layer transition on a cone-cylinder-flare configuration[J]. Journal of Experiments in Fluid Dynamics, 2013, 27(6):26-31. DOI: 10.3969/j.issn.1672-9897.2013.06.005
[13] Park C. Assessment of two-temperature kinetic model for dissociating and weakly-ionizing nitrogen[J]. Journal of Thermophysics and Heat Transfer, 1988, 2(1):8-16. DOI: 10.2514/3.55
[14] Kay R D, Netterfield M P. Thermochemical non-equilibrium computations for a Mars entry vehicle[R]. AIAA-93-2841, 1993. DOI: 10.2514/6.1993-2841
[15] Suzuki K, Abe T. Thermochemical nonequilibrium viscous shock-layer analysis for a Mars aerocapture vehicle[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(4):773-780. DOI: 10.2514/3.611
[16] Furudate M, Suzuki T, Takayanagi H, et al. Three-dimensional aerodynamics study for Mars aeroshellin nonequilibrium flow[R]. AIAA-2010-4647, 2010. DOI: 10.2514/6.2010-4647
[17] 柳森, 黄洁, 李毅, 等.中国空气动力研究与发展中心的空间碎片超高速撞击试验研究进展[J].载人航天, 2011, 17(6):17-23. DOI: 10.3969/j.issn.1674-5825.2011.06.004 Liu S, Huang J, Li Y, et al. Recent advancement of hypervelocity impact tests at HAI[J]. Journal of Manned Spacecraft, 2011, 17(6):17-23. DOI: 10.3969/j.issn.1674-5825.2011.06.004
[18] Park C, Howe J, Jaffe R, et al. Review of chemical-kinetic problems of future NASA missions, Ⅱ:Mars entries[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1):9-23. DOI: 10.2514/3.496
[19] 董维中.气体模型对高超声速再入钝体气动参数计算影响的研究[J].空气动力学学报, 2001, 19(2):197-202. DOI: 10.3969/j.issn.0258-1825.2001.02.010 Dong W Z. Thermal and chemical model effect on the calculation of aerodynamic parameter for hypersonic reentry blunt body[J]. Acta Aerodynamica Sinica, 2001, 19(2): 197-202. DOI: 10.3969/j.issn.0258-1825.2001.02.010






 下载:
下载: