Research on mechanism of transonic area rule in near field
-
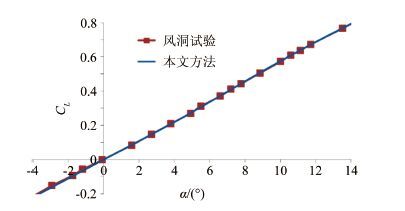
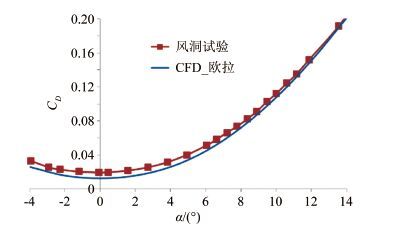
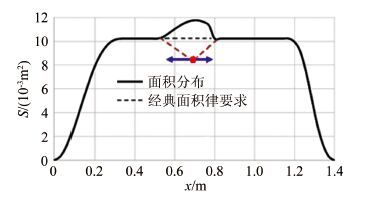
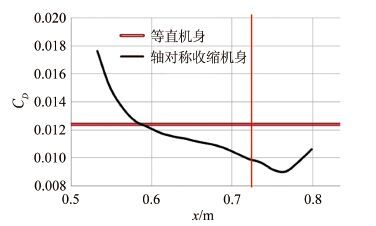
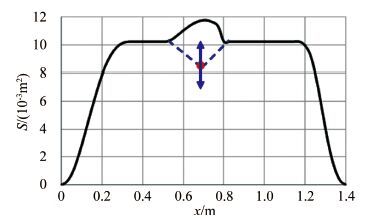
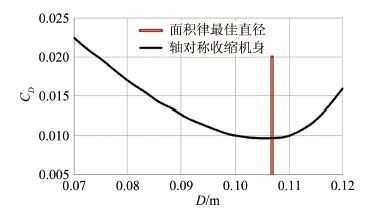
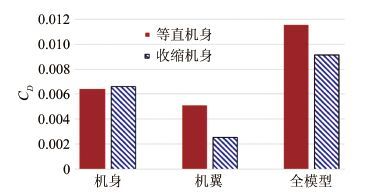
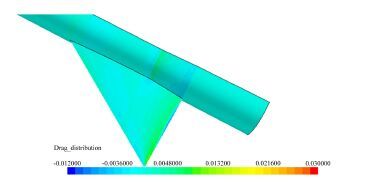
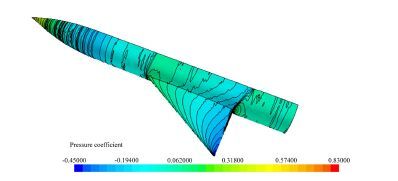
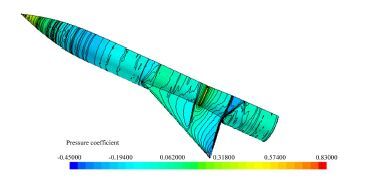
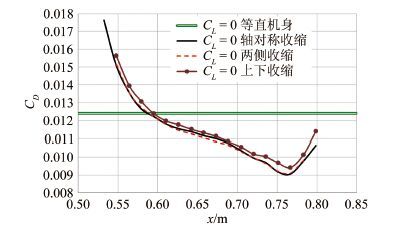
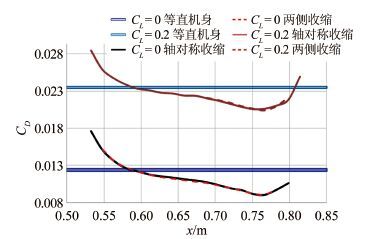
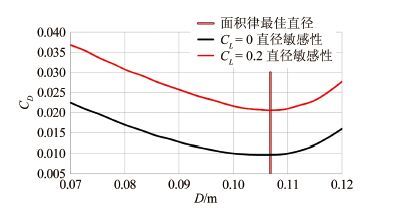
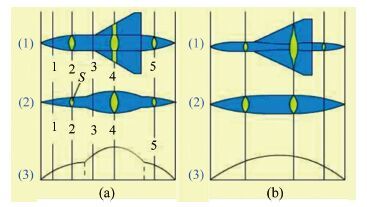
摘要: 面积律过于定性的描述给实际的飞机设计工作带来了一定的困惑和问题，其理论推导采用的小扰动线化假设也不适应未来空气动力学设计越来越精细化的发展方向。针对具有典型高速飞行器外形特征的AGARD-B标模，结合CFD和优化方法，探讨了实现最优减阻效果的机身修形形式，得出了较经典跨声速面积律减阻效果更好的结果，给出了比经典面积律更为细致的减阻修形原则。以此为基础，通过对各部件的减阻贡献情况的分析，通过修形前后机体表面阻力、压强及等压线分布的对比，发现面积律减阻的实质是飞行器外形所造成的相邻部件之间的压力传递而形成的有利干扰。应用这一结论，研究并验证了机身收缩剖面形状对于减阻效果的影响。最后经过不同升力系数条件的对比，证明对于不同升力、不同迎角的飞行条件，面积律减阻的效果是相同的。Abstract: The qualitative descriptions of the area rule bring some confusion and problems to the actual aircraft design work. The linear perturbation assumption in conventional theoretical derivations does not suit the development for more and more refined aerodynamic design in the future. For AGARD-B standard model which has typical shape characteristics of high speed aircraft, we combined the CFD with optimization methods to probe the body modification form for optimal drag reduction. From that, a better drag reduction result and more detailed modification principles of drag reduction are obtained compared to those obtained from the traditional area rule method. Based on the present principles, through the analysis of drag force felt by each component and comparison of the drag forces on the body surface before and after modification, it is found that the essence of area rule drag reduction is the advantageous interference produced among the adjacent components of the aircraft configuration. Finally, the drag reduction effects of fuselage shrinkage cross-sectional shape are studied and verified. The comparison among different lift coefficient conditions validates that the drag reduction effect of area rule is the same under various lift coefficients and angles of attack condition.
-
Keywords:
- area rule /
- flow mechanism /
- aircraft design /
- aerodynamics /
- computational fluid mechanics /
- interference drag
-
-
![]()
图 8 阻力随机身最大收缩直径所在位置的变化
Fig. 8 Drag varies with fuselage location of maximum contraction diameter
![]()
图 9 改变机身最大收缩直径的计算数模横截面积分布
Fig. 9 Cross section distribution of geometry model for changing fuselage maximum reducing diameter
![]()
图 10 不同机身最大收缩直径对减阻效果的影响
Fig. 10 Drag reduction with various minimal fuselage diameter after contraction
![]()
图 11 面积律减阻前后各部件阻力贡献对比
Fig. 11 Comparison of drag contributions of different components with/without area rule
![]()
图 16 3种收缩机身导致的阻力随机身最大收缩面积所在位置的变化
Fig. 16 Drag comparison for three kinds of fuselage with location of maximum contraction area
![]()
图 17 不同升力系数下阻力随机身最大收缩面积所在位置的变化
Fig. 17 Drag comparison for varying lift with fuselage location of maximum contraction area
![]()
图 18 不同升力系数下阻力随机身最大收缩面积位置的变化
Fig. 18 Variational drag for varying lift with various minimal fuselage diameter after contracion
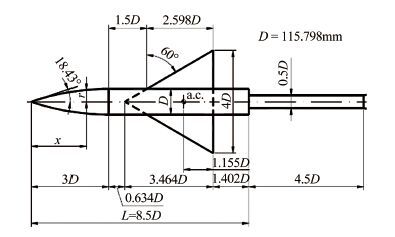
表 1 AGARD-B标准模型参数
Table 1 Parameters of standard model AGARD-B
参数 值 参考面积 0.0929m2 机翼前缘后掠角 60° 机翼展弦比 2.31 机翼相对厚度 4% 机身长细比 8.5 机头长细比 3 翼型 双圆弧翼型 翼型最大厚度位置 50%弦长 
下载: 导出CSV
-
[1] Cole J D, Cook L P. Transonic aerodynamics[M]. Amsterdam: Elsevier Science Publishers, 2012.
[2] Chattot J, et al. Theoretical and applied aerodynamics[M]. New York: Springer Science+Business Media, 2015.
[3] Gu Y Q, Fan T X, Mou J G, et al. Drag reduction technology of jet-a review[J]. International Journal of Engineering Research in Africa, 2015, 17(7): 30-42. http://cn.bing.com/academic/profile?id=2243434047&encoded=0&v=paper_preview&mkt=zh-cn
[4] Jameson A, Ou K. 50 years of transonic aircraft design[J]. Progress in Aerospace Sciences, 2011, 47(5): 308-318. DOI: 10.1016/j.paerosci.2011.01.001
[5] David A. Computational sensitivity analysis for the aerodynamic design of supersonic and hypersonic air vehicles[R]. ADA622380, 2015. http://cn.bing.com/academic/profile?id=2195423499&encoded=0&v=paper_preview&mkt=zh-cn
[6] Michael G. Computational analysis and characterization of RC-135 external aerodynamics[R]. ADA561659, 2012.
[7] Forbes A, Patel A, Cone C, et al. Drag prediction for supersonic hydrogen-fueled airliners[R]. AIAA-2011-3968, 2011.
[8] Palaniappan K, Jameson A. Bodies having minimum pressure drag in supersonic flow: Investigating nonlinear effects[J]. Journal of Aircraft, 2010, 47(4): 1451-1454. DOI: 10.2514/1.C031000
[9] Dehpanah P, Nejat A. The aerodynamic design evaluation of a blended-wing-body configuration[J]. Aerospace Science and Technology, 2015, 43(6): 96-110. http://cn.bing.com/academic/profile?id=2037238279&encoded=0&v=paper_preview&mkt=zh-cn
[10] Lyu Z, Joaquim R, Martins R. Aerodynamic design optimization studies of a blended-wing-body aircraft[J]. Journal of Aircraft, 2014, 51(5): 1604-1617. DOI: 10.2514/1.C032491
[11] Roysdon P, Khalid M. Lateral-directional stability investigation of a blended-wing-body[R]. AIAA-2010-9617, 2010.
[12] Utsumi Y, Obayashi S. Design of supersonic biplane aircraft concerning sonic boom minimization[R]. AIAA-2010-4962, 2010. http://cn.bing.com/academic/profile?id=2171865953&encoded=0&v=paper_preview&mkt=zh-cn
[13] Ku Y C, Rho J H, et al. Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave[J]. Structural and Multidisciplinary Optimization, 2010, 42(6): 965-976. DOI: 10.1007/s00158-010-0550-6
[14] Alyanak E. Modeling for conceptual design: an aeroelastic approach[R]. AIAA-2012-1425, 2012.
[15] Christopher L O, Choi S. Design of optimum equivalent-area target for high-fidelity low-boom aircraft design[R]. AIAA-2015-2580, 2015.
[16] Khalid A, Kumar P. Aerodynamic optimization of box wing-a case study[J]. International Journal of Aviation, Aeronautics, and Aerospace, 2014, 1(4): 1-46. http://cn.bing.com/academic/profile?id=127845652&encoded=0&v=paper_preview&mkt=zh-cn
[17] Berger C, Carmona K, et al. Supersonic bi-directional flying wing configuration with low sonic boom and high aerodynamic efficiency[R]. AIAA-2011-3663, 2011. http://www.researchgate.net/publication/268004294_Supersonic_Bi-Directional_Flying_Wing_Configuration_with_Low_Sonic_Boom_and_High_Aerodynamic_Efficiency
[18] Zha G, Im H, Espinal D. Toward zero sonic-boom and high efficiency supersonic flight, part i: a novel concept of supersonic bi-directional flying wing[R]. AIAA-2010-1013, 2010.
[19] Wintzer M, Kroo I. Optimization and adjoint-based CFD for the conceptual design of low sonic boom aircraft[R]. AIAA-2012-963, 2012.
[20] Waddington M, McDonald R. Development of an interactive wave drag capability for the open VSP parametric geometry tool[R]. AIAA-2015-2548, 2015.
[21] Guan X H. Supersonic wing-body two-level wave drag optimization using extended far-field composite-element methodology[J]. AIAA Journal, 2014, 52(5): 981-990. DOI: 10.2514/1.J052305
[22] Feng X Q, Li Z K, et al. Research of low boom and low drag supersonic aircraft design[J]. Chinese Journal of Aeronautics, 2014, 27(3): 531-541. DOI: 10.1016/j.cja.2014.04.004
[23] Berci M, Vigevano L. Sonic boom propagation with a non linear geometrical acoustic model[R]. AIAA-2011-2856, 2011.
[24] Berci1 M, Igevano L. Sonic boom propagation revisited: a nonlinear geometrical acoustic model[J]. Aerospace Science and Technology, 2012, 23(1): 280-295. DOI: 10.1016/j.ast.2011.08.003
[25] Haas A, Kroo I. A multi-shock inverse design method for low-boom supersonic aircraft[R]. AIAA-2010-843, 2010.
[26] Jung T, Starkey R, et al. Design methods to create frozen sonic booms via lobe balancing using aircraft components[R]. AIAA-2011-2857, 2011.
[27] Damljanovic D, Vitic A, et al. Testing of AGARD-B calibration model in the T-38 transonic wind tunnel[J]. Scientific Technical Review, 2006, 56(2): 52-62.
计量
- 文章访问数: 194
- HTML全文浏览量: 148
- PDF下载量: 13
