AI-based real-time noise reduction of flow field pressure signals under plasma electromagnetic interference
-
摘要: 面向闭环主动流动控制的可靠传感需求,提出采用人工神经网络模型对不同等离子体电磁干扰下受污染流场信号进行实时降噪处理。以安装在圆柱表面的动态压力传感器为研究对象,分别采集了正弦交流介质阻挡放电(AC–DBD)的“稠密峰”型干扰信号和纳秒脉冲介质阻挡放电(NS–DBD)的“稀疏突刺”型干扰信号,对人工合成含干扰的流场压力数据进行了监督学习训练,并对模型的泛化能力进行了测试验证。结果表明:基于人工神经网络模型的实时降噪方法可以有效抑制等离子体激励带来的电磁干扰影响,还原真实的压力信号,且对AC–DBD“稠密峰”型干扰信号的降噪效果更好,降噪后信号波形平滑,与真实信号拟合度高;将模型用于真实的流场压力测量中,通过对比降噪后信号与真实信号均值,验证了降噪神经网络的信号还原精度。Abstract: For the reliable sensing requirements of closed-loop active flow control, a real-time noise reduction method based on the artificial neural network was proposed for solving the plasma actuation electromagnetic interference on flow field signals. Taking the dynamic pressure sensor installed on the cylinder surface as the experimental subject, the “dense peak” type noise signals of alternating current dielectric barrier discharge (AC–DBD) and the “sparse spike” type noise signals of nanosecond pulsed dielectric barrier discharge (NS–DBD) were collected respectively. Artificial synthetic noise signals were used for supervised learning, and the generalization of the artificial neural network model was tested and verified. The results show that this method can effectively suppress the influence of electromagnetic interference caused by plasma actuation and restore the real pressure signal. It has better denoising performance on the AC–DBD “dense peak” type noise signal. The denoised signal is smoother and better fitted with the real one. This model is also applied to the real flow field pressure measurement, and the accuracy of the denoising network prediction is further verified by comparing the mean value of the denoised signal and the real signal.
-
0 引 言
主动流动控制对于解决关键气动问题具有重要作用[1-3]。沿面介质阻挡放电作为一种有效的等离子体流动控制技术,具有频带宽、响应迅速、结构简单等特点,在湍流边界层减阻[4-7]、旋涡控制[8-11]、分离控制[12-15]、防除冰[16-19]等方面展现出巨大的应用潜力,受到了国内外研究者的广泛关注。当前,等离子体流动控制研究大都为开环控制,基于流场状态对等离子体激励强度进行闭环自适应调节是未来研究的发展趋势。但等离子体激励器的高压脉冲电流会对传感器工作造成强电磁干扰,即便进行了良好的接地,传感器采集的信号仍会受到严重污染,突出表现为信号时均值飘移、出现极高幅值的“突刺”,所占据的频谱范围与流场信号重叠,很难将此类干扰信号滤除,这对等离子体流动控制的实验研究与工程应用都带来了严峻挑战。
近年来,随着机器学习的不断发展,深度学习被大量应用于图像降噪之中[20]。巨大的模型容量和精心设计的网络架构赋予了这些图像去噪网络极强的模式表达和拟合能力,使其能够对大规模数据集中蕴含的图像恢复规律进行学习[21-24]。借助机器学习,是否可以在大规模数据中习得含干扰噪声信号的降噪规律,实现等离子体电磁干扰下流场信号的智能实时降噪?针对这一问题,本文提出一种基于人工神经网络模型的实时降噪方法,以动态压力传感器为对象,选取研究最为广泛的正弦交流介质阻挡放电(AC–DBD)与纳秒脉冲介质阻挡放电(NS–DBD)进行实验研究,人工合成含干扰的流场压力数据进行训练测试,最后将训练好的模型在真实流场压力测量中进行验证。
1 实验系统及方法
1.1 实验系统
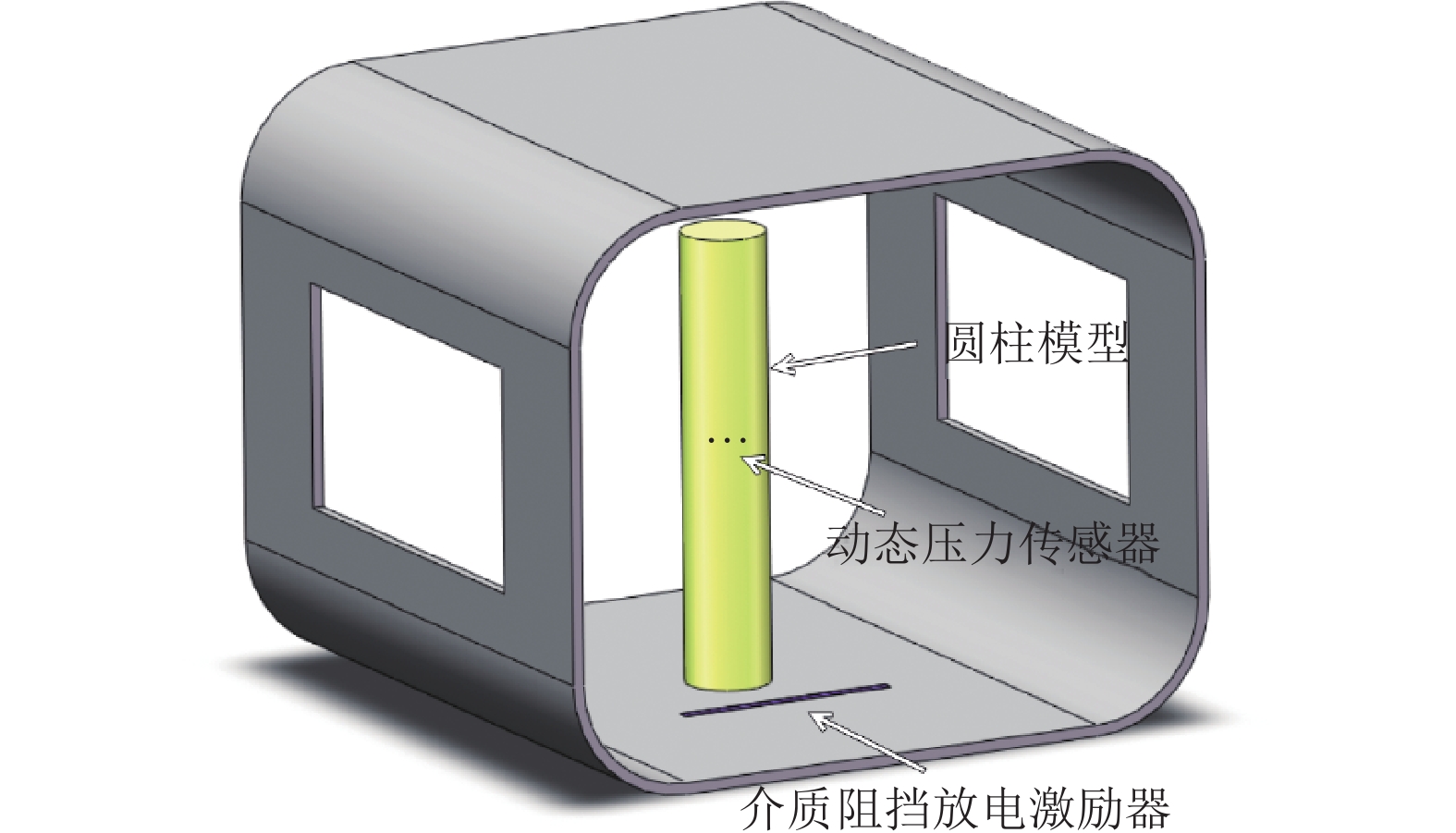
实验基于圆柱绕流开展。风洞试验段尺寸为1.2 m × 1.0 m,来流风速0~75 m/s可调,主流区湍流度 ≤ 0.2%。圆柱模型竖直安装于试验段,底部用螺丝与底壁紧固(图1)。模型直径D = 150 mm,高度H = 800 mm,材料选用ABS工程塑料。动态压力传感器安装于模型中段,用于测量流场压力变化,型号为ALX314,量程为0~2 kPa,精度为0.25% F.S.,输出信号为0~5 V三线制标准模拟信号,信号放大采用差动输入式仪表放大器。压力信号数据由LabVIEW程序配合NI PCI–6014采集卡进行采集存储。
等离子体激励系统由介质阻挡放电激励器和高压电源组成,如图2所示。为防止等离子体激励改变流场状态、增加压力测量的不确定性,激励器安装于风洞试验段底壁、圆柱模型下游200 mm(图1)处。激励器由高压电极、绝缘介质层、覆盖电极组成,电极为5 mm宽的铜箔胶带,绝缘介质层为厚0.12 mm的聚酰亚胺,介电常数为3.4。
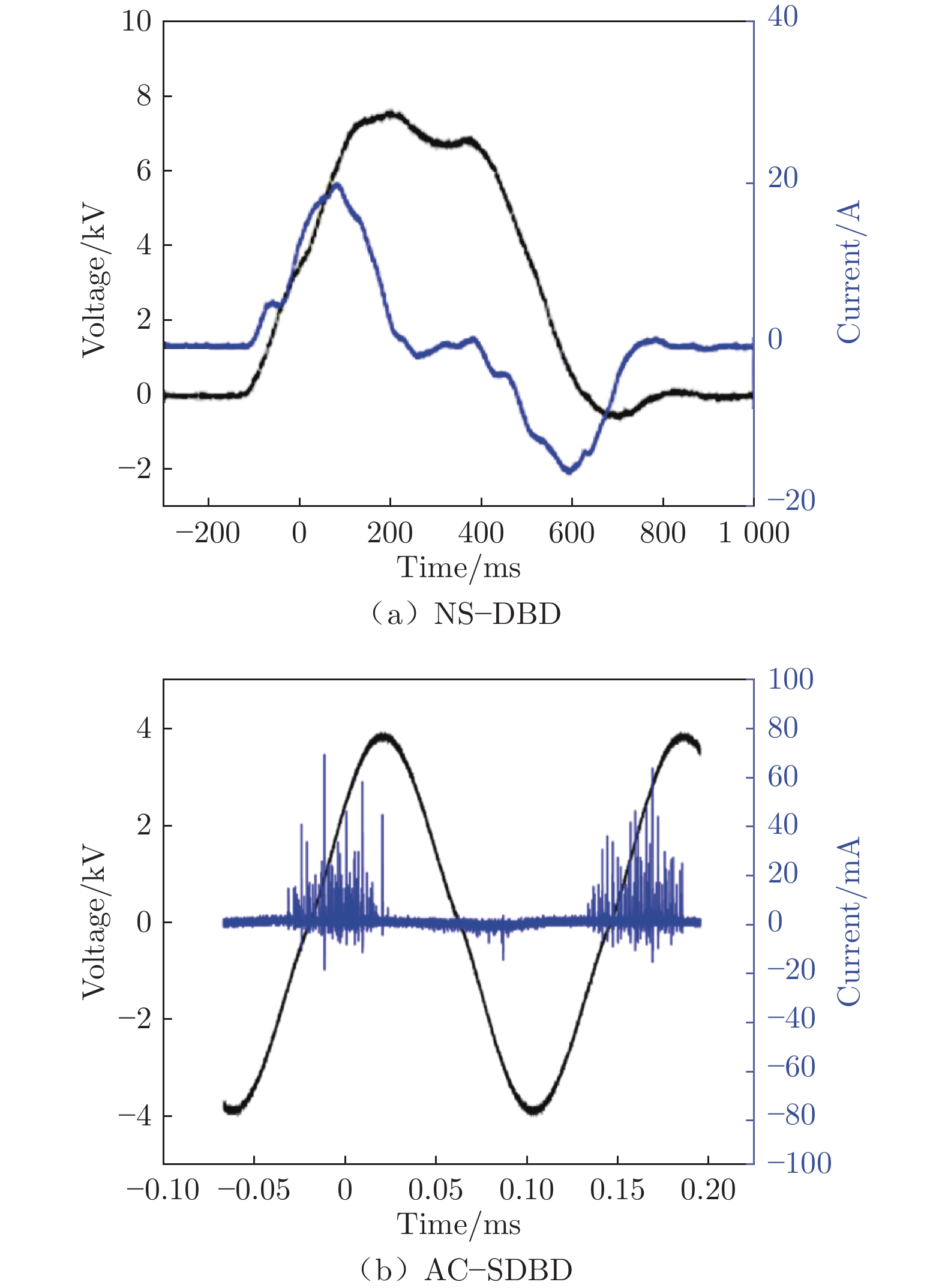
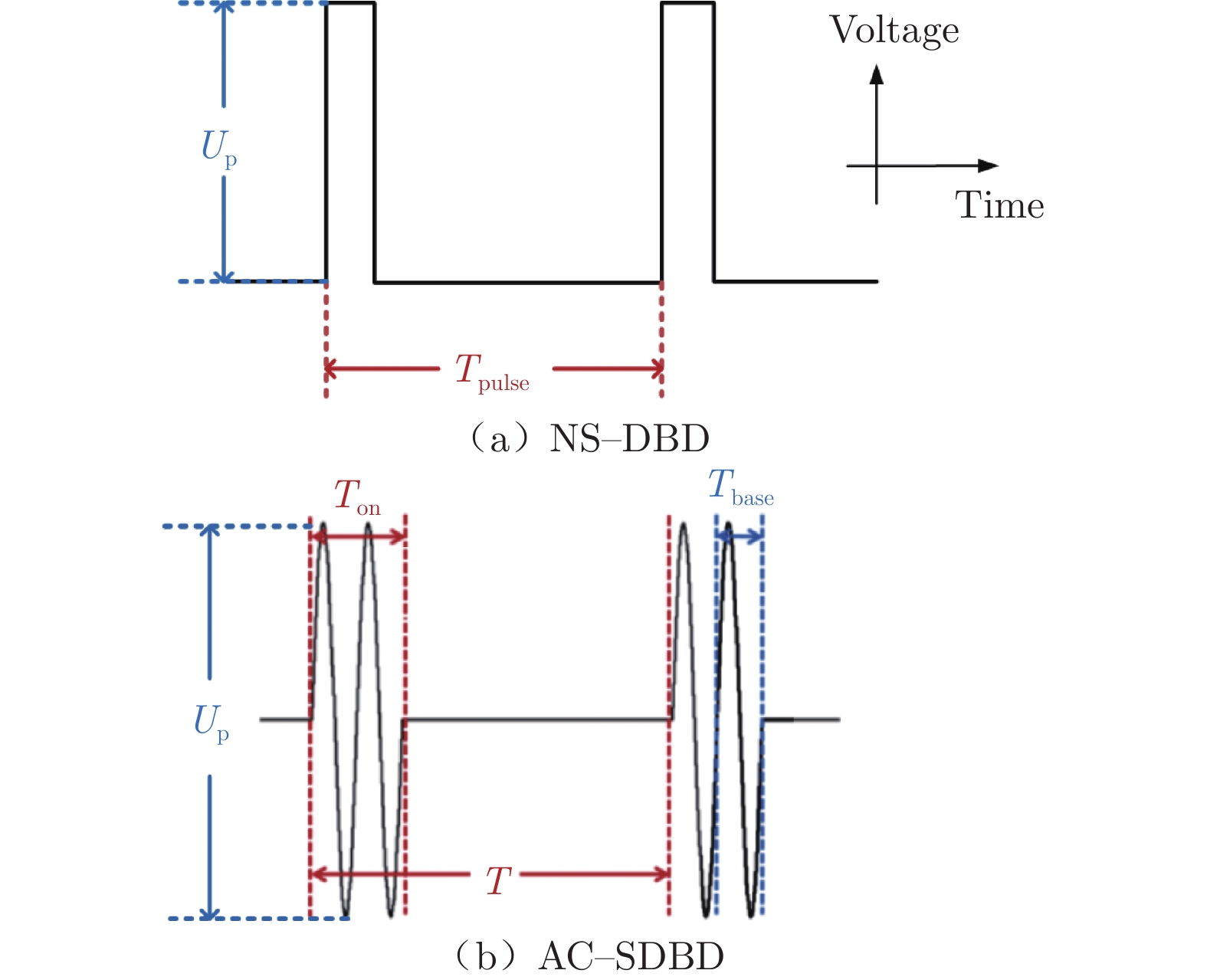
根据高压激励电源的不同,介质阻挡放电分为 AC–DBD(由Electrofluidsystems Minipulse 2.0高压正弦波电源驱动)和NS–DBD(由双极性高性能纳秒刀脉冲电源HVP–B3000/IRE驱动)。DPO4104示波器、P6015A高压探针和TCP0030A电流探针用于测量等离子体激励放电时的电压、电流等参数。实验中测得的NS–DBD和 AC–DBD典型电压、电流波形如图3所示。激励电压波形如图4所示,图中Up为电压峰值、Tpulse为脉冲电压的脉宽时间,Tbase为正弦波电压的载波周期,Ton为一个调制周期内等离子体激励时间,T为正弦波电压的调制周期。本文电压峰值Up、载波频率fbase(fbase = 1/Tbase)、调制频率fm (fm = 1/T)、脉冲频率fp(fp = 1/Tpulse)均可调。占空比DC(Duty Cycle)= Ton/T,在实验中固定为50%。另外,为了防止产生共地干扰,利用隔离变压器将等离子体激励系统与数据采集系统隔离开。
1.2 实验方法
本文提出采用人工神经网络模型对不同等离子体电磁干扰下受污染流场信号进行降噪,即将电磁干扰下测得的含干扰压力数据作为输入,输出真实的压力数据。由于在实验过程中无法同时获得含干扰的压力信号和干净的压力信号作为标签进行学习,本文基于加性噪声模型假设,人工构造噪声信号和真实信号(图5),记无干扰的干净压力数据(即真实信号)为$ S(t) $,而与之对应的干扰噪声(即噪声信号)为$ N(t) $,则含干扰的压力信号(简称含干扰信号)可表示为:
$$ Y(t) = S(t) + N(t) $$ (1) 通过学习提供的样本数据,对神经网络模型中的参数进行更新,使得模型对新输入的含干扰信号$ Y(t) $的处理结果尽可能逼近真实信号,即对$ Y(t) $中的噪声信号$ N(t) $进行压制并恢复其中所含的真实信号$ S(t) $:
$$ Y(t) \to S(t): \mathop {\arg \min }\limits_{\theta \in \Theta } E\{{[\mathop {Y(t) - }\limits^ \wedge S(t)]^2}\} $$ (2) 式中:θ表示神经网络参数,$\Theta $表示参数的范围域。
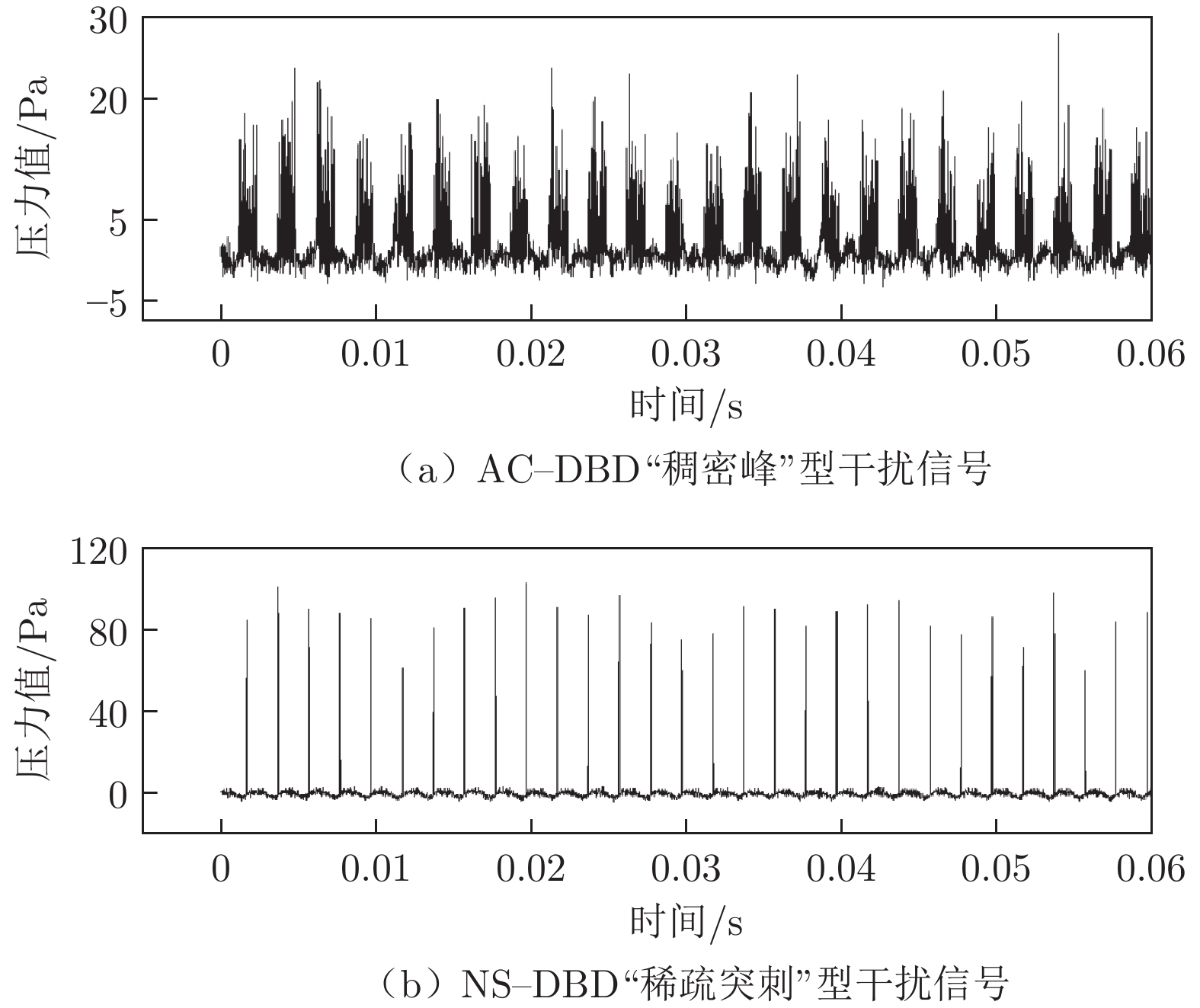
首先,在无来流条件下,以不同的电参数施加等离子体激励,测得相应的噪声信号$ N(t) $,采样频率为40 kHz,采样时间为30 s,得到 AC–DBD “稠密峰”型干扰信号与NS–DBD “稀疏突刺”型干扰信号,如图6所示。随后,关闭等离子体激励,在不同的来流速度下随机采集真实信号$ S(t) $,采样频率和采样时间与采集噪声信号时相同。人工合成含干扰信号$ Y(t) $,将$ Y(t) $与真实信号$ S(t) $以每组400个采样点分组进行训练。
人工神经网络模型选用6层网络结构。网络输入包括电参数特征及分段的含干扰信号$ Y(t) $,输出为分段的真实信号$ S(t) $。网络模型参数设置如表1所示,其中输入层节点数是关键参数之一,NS–DBD预测模型输入层节点数选为402个(脉冲电压值Up、脉冲频率fp和400个含干扰信号数据点); AC–DBD预测模型输入层节点数选为403个(电压峰值Up、载波频率fbase、调制频率fm和400个含干扰信号数据点)。
表 1 人工神经网络模型参数Table 1 Parameters of artificial neural network model网络模型参数 设置值 输入层节点数 402(NS–DBD),403(AC–DBD) 隐含层数 4 隐含层节点数 512,1024,2048,1024 输出层节点数 400 激活函数 Leaky ReLU 优化器 Adam 损失函数 均方根误差(RMSE) 初始学习率 0.001 学习率衰减系数 0.96 2 实验内容
2.1 模型训练
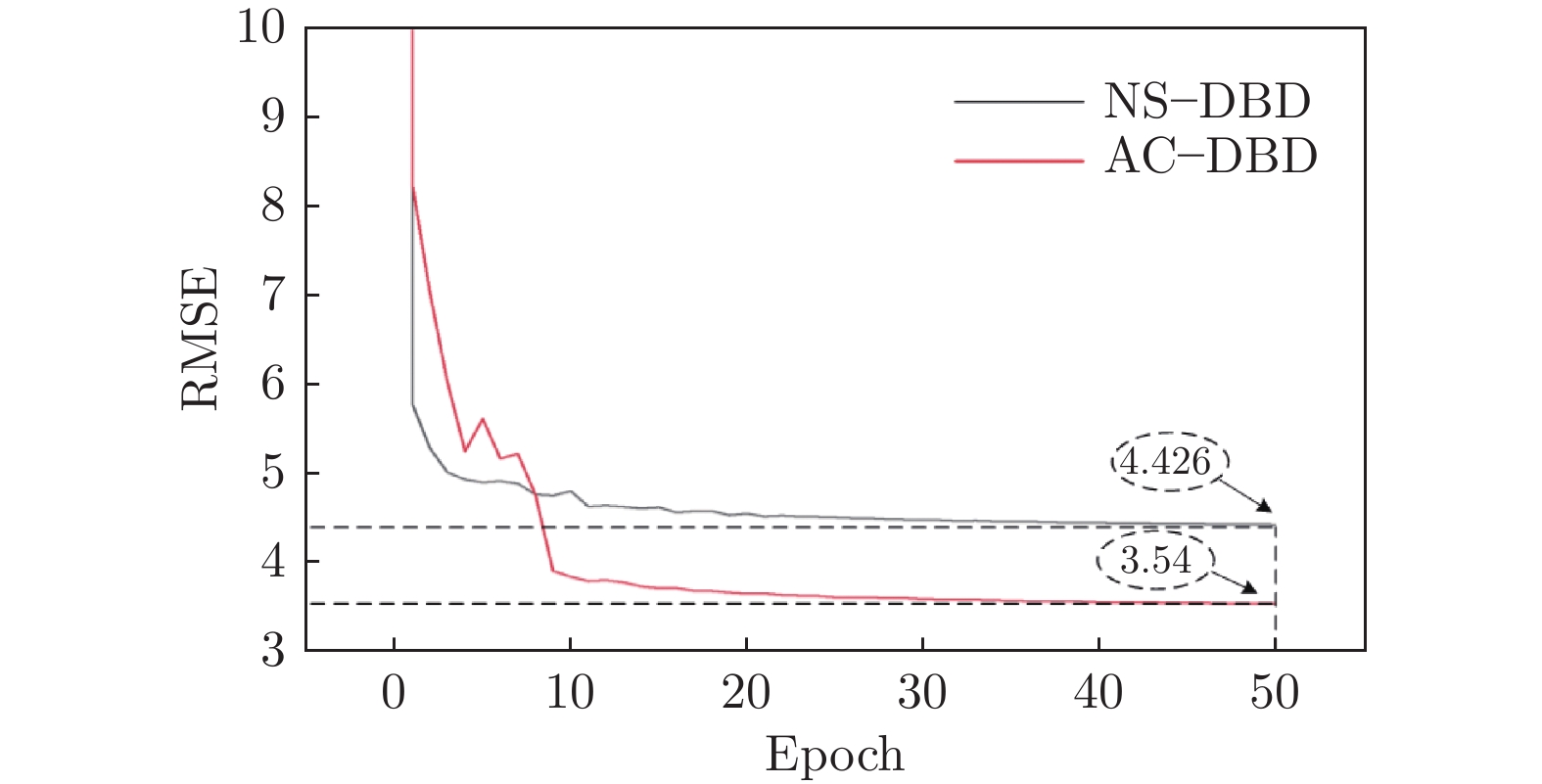
将Batch Size(一次训练所选取的样本数)设置为400,Epoch(使用训练集全部样本训练一次即为1个Epoch)数设置为50,选取不同电参数激励下 AC–DBD与NS–DBD采集的动态压力信号进行模型训练,电参数如表2、3所示,其中NS–DBD施加电压上升沿时间设置为150 ns、脉宽设置为50 ns、下降沿时间设置为150 ns。
表 2 AC–DBD模型训练电参数Table 2 Electrical parameters of training data for AC–DBD model电压Up/kV 载波频率fbase/kHz 调制频率fm/Hz 4,6,8,10,12 6,8,10,12 100,300,500,700,900 表 3 NS–DBD模型训练电参数Table 3 Electrical parameters of training data for NS–DBD model电压Up/kV 脉冲频率fp/Hz 4,6,8,10,12 200,400,600,800,1000,1200,1400 图7 为人工神经网络训练损失曲线。可以看到,前10次Epoch损失曲线急剧下降,10次以后网络趋于收敛,网络训练损失几乎不再减小,NS–DBD均方根误差最后收敛约4.426,AC–DBD均方根误差最后收敛于约3.54。需要指出的是,动态压力传感器量程为0~2 kPa,精度0.25% F.S.,传感器误差允许范围为5 Pa,若降噪后信号与真实信号的均方根误差小于5,即认为降噪后信号与真实信号拟合较好,在误差允许的范围内。取Epoch为50的网络作为最终模型,用于降噪测试验证。
2.2 模型验证
2.2.1 合成信号还原
采用上述训练好的模型对不同电参数下的含干扰信号进行降噪还原,同时,为验证神经网络的泛化能力,将训练集中不包含的电参数用于测试。 AC–DBD模型的测试参数设置如表4所示。
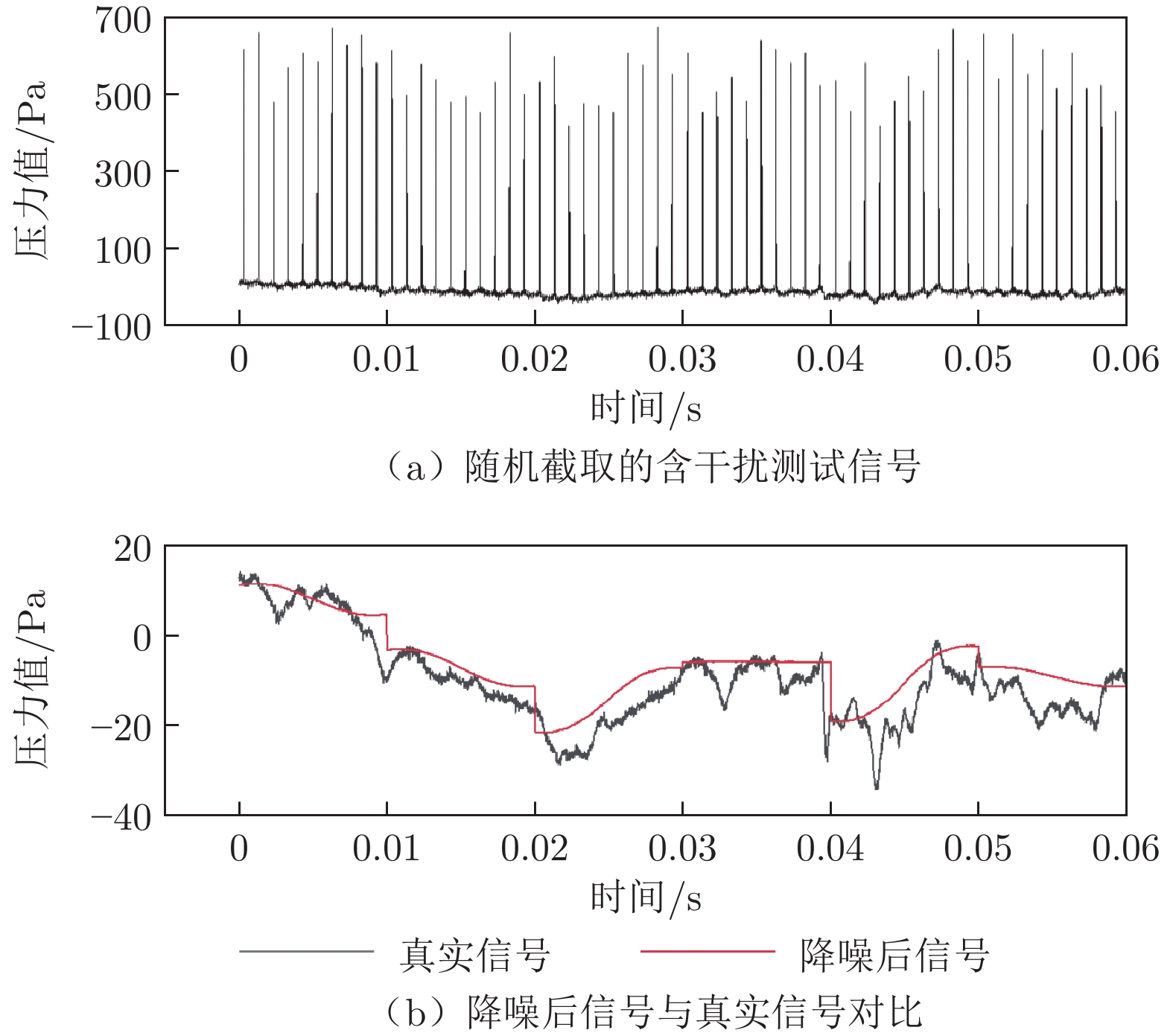
表 4 AC–DBD模型测试电参数Table 4 Electrical parameters of testing data for AC–DBD model电压Up/kV 载波频率fbase/kHz 调制频率fm/Hz 5,7,9,11 5,7,9,11 200,400,600,800,1000 图8(a)为随机截取的含干扰信号。用训练好的模型进行还原后,与真实信号对比,如图8(b)所示,降噪前的压力信号在−30~0 Pa之间剧烈脉动,周期性出现“稠密峰”,降噪后压力信号波形更加平滑,与真实信号拟合较好。分别计算不同激励电参数下的降噪前后信号与真实信号的均方根误差(记降噪前信号与真实信号的均方根误差为RMSE1,降噪后信号与真实信号的均方根误差为RMSE2),如表5所示,由于电磁干扰导致压力信号均值发生飘移、出现“稠密峰”,RMSE1均在30以上,且数值大小与电压峰值Up、载波频率fbase、调制频率fm均正相关,数值越大表示电磁干扰越强;降噪后 RMSE2均在误差允许范围内。对于训练集中未涉及的电参数,也能够很好地进行还原,这表明神经网络泛化性较好,适用性更强。
表 5 不同电参数下AC–DBD模型降噪前后均方根误差Table 5 RMSE value of AC–DBD model under different testing electrical parameters激励电参数 RMSE1 RMSE2 Up = 5 kV,fbase = 7 kHz,fm = 200 Hz 32.86 3.73 Up = 5 kV,fbase = 9 kHz,fm = 400 Hz 39.56 3.27 Up = 5 kV,fbase = 11 kHz,fm = 600 Hz 42.22 3.66 Up = 7 kV,fbase = 7 kHz,fm = 400 Hz 40.23 2.89 Up = 7 kV,fbase = 9 kHz,fm = 600 Hz 44.10 3.12 Up = 7 kV,fbase = 11 kHz,fm = 800 Hz 48.36 3.24 Up = 9 kV,fbase = 7 kHz,fm = 600 Hz 48.30 3.36 Up = 9 kV,fbase = 9 kHz,fm = 800 Hz 56.23 3.78 Up = 9 kV,fbase = 11 kHz,fm = 1000 Hz 62.35 3.82 Up = 11 kV,fbase = 7 kHz,fm = 800 Hz 66.23 2.99 Up = 11 kV,fbase = 9 kHz,fm = 1000 Hz 70.51 3.64 Up = 11 kV,fbase = 11 kHz,fm = 200 Hz 66.16 2.81 NS–DBD模型的测试参数设置如表6所示。随机截取的含干扰信号如图9(a)所示,采用训练好的模型进行降噪后,与真实信号进行对比,如图9(b)所示,降噪前信号周期性出现500~700 Pa的“突刺跳跃”,降噪后大致可以拟合出真实信号的变化趋势,但局部还会出现阶跃。对比不同测试参数下降噪前后信号与真实信号的均方根误差(表7),可以看到,与 AC–DBD类似,RMSE1与电压峰值Up、脉冲频率fp 正相关;降噪后RMSE2相比AC–DBD较大,但也在误差允许范围内。
表 6 NS–DBD模型测试电参数Table 6 Electrical parameters of testing data for NS–DBD model电压Up/kV 脉冲频率fp/Hz 5,7,9,11 300,500,700,900,1100 表 7 不同电参数下NS–DBD模型降噪前后均方根误差Table 7 RMSE value of NS–DBD model under different testing electrical parameters激励电参数 RMSE1 RMSE2 Up = 5 kV,fp = 300 Hz 40.36 4.36 Up = 5 kV,fp = 500 Hz 51.63 4.89 Up = 5 kV,fp = 700 Hz 62.22 4.78 Up = 7 kV,fp = 500 Hz 50.24 4.86 Up = 7 kV,fp = 700 Hz 59.33 4.88 Up = 7 kV,fp = 900 Hz 68.36 4.98 Up = 9 kV,fp = 700 Hz 66.32 4.48 Up = 9 kV,fp = 900 Hz 72.56 4.36 Up = 9 kV,fp = 1100 Hz 79.85 4.90 Up = 11 kV,fp = 300 Hz 68.49 4.22 Up = 11 kV,fp = 900 Hz 90.22 4.23 Up = 11 kV,fp = 1100 Hz 105.62 4.58 2.2.2 实测信号还原
进一步对实测的干扰信号进行研究,在10 m/s的稳定来流下,分别测得含干扰的压力信号和无干扰的压力信号,并利用训练好的模型进行降噪,对比1 s内降噪后的压力平均值与干净压力信号的平均值,如表8所示,NS–DBD模型降噪后均值差大于 AC–DBD模型,但均在3 Pa以内,侧面印证了该模型能够有效抑制干扰噪声,可应用于实际测量。
表 8 降噪后的压力信号均值与干净压力信号均值对比Table 8 Mean value comparison between the denoised pressure signal and the clean pressure signal激励电参数 降噪后信号与
真实信号的
均值差/PaAC–DBD Up = 5 kV,fbase = 6 kHz,fm = 200 Hz 1.26 Up = 5 kV,fbase = 8 kHz,fm = 400 Hz 1.15 Up = 7 kV,fbase = 6 kHz,fm = 400 Hz 1.36 Up = 7 kV,fbase = 8 kHz,fm = 600 Hz 1.44 Up = 9 kV,fbase = 6 kHz,fm = 600 Hz 1.52 Up = 9 kV,fbase = 8 kHz,fm = 800 Hz 1.21 Up = 11 kV,fbase = 6 kHz, fm = 800 Hz 1.58 Up = 11 kV,fbase = 8 kHz, fm = 1000 Hz 1.61 NS–DBD Up = 6 kV,fp = 200 Hz 2.98 Up = 7 kV,fp = 300 Hz 2.32 Up = 8 kV,fp = 400 Hz 2.36 Up = 9 kV,fp = 500 Hz 2.22 Up = 10 kV,fp = 600 Hz 2.43 Up = 11 kV,fp = 700 Hz 2.58 Up = 13 kV,fp = 800 Hz 2.46 Up = 14 kV,fp = 900 Hz 2.77 3 结 论
本文基于加性噪声模型假设,利用人工神经网络对等离子体电磁干扰下圆柱绕流壁面压力信号进行降噪,人工合成含干扰的流场压力数据进行监督学习训练,并对模型进行了验证,得到如下结论:
1)本文方法能够有效消除等离子体激励电磁干扰的影响,还原真实的压力信号,且对AC–DBD的“稠密峰”型干扰信号的降噪效果比对NS–DBD的“稀疏突刺”型干扰信号的降噪效果更好,降噪后与原信号拟合更好,波形更加平滑。
2)使用本文提出的抑制电磁干扰的方法,需要提供相应的电参数,还需进一步研究普适的神经网络结构,使其不依赖于电参数。
-
表 1 人工神经网络模型参数
Table 1 Parameters of artificial neural network model
网络模型参数 设置值 输入层节点数 402(NS–DBD),403(AC–DBD) 隐含层数 4 隐含层节点数 512,1024,2048,1024 输出层节点数 400 激活函数 Leaky ReLU 优化器 Adam 损失函数 均方根误差(RMSE) 初始学习率 0.001 学习率衰减系数 0.96 表 2 AC–DBD模型训练电参数
Table 2 Electrical parameters of training data for AC–DBD model
电压Up/kV 载波频率fbase/kHz 调制频率fm/Hz 4,6,8,10,12 6,8,10,12 100,300,500,700,900 表 3 NS–DBD模型训练电参数
Table 3 Electrical parameters of training data for NS–DBD model
电压Up/kV 脉冲频率fp/Hz 4,6,8,10,12 200,400,600,800,1000,1200,1400 表 4 AC–DBD模型测试电参数
Table 4 Electrical parameters of testing data for AC–DBD model
电压Up/kV 载波频率fbase/kHz 调制频率fm/Hz 5,7,9,11 5,7,9,11 200,400,600,800,1000 表 5 不同电参数下AC–DBD模型降噪前后均方根误差
Table 5 RMSE value of AC–DBD model under different testing electrical parameters
激励电参数 RMSE1 RMSE2 Up = 5 kV,fbase = 7 kHz,fm = 200 Hz 32.86 3.73 Up = 5 kV,fbase = 9 kHz,fm = 400 Hz 39.56 3.27 Up = 5 kV,fbase = 11 kHz,fm = 600 Hz 42.22 3.66 Up = 7 kV,fbase = 7 kHz,fm = 400 Hz 40.23 2.89 Up = 7 kV,fbase = 9 kHz,fm = 600 Hz 44.10 3.12 Up = 7 kV,fbase = 11 kHz,fm = 800 Hz 48.36 3.24 Up = 9 kV,fbase = 7 kHz,fm = 600 Hz 48.30 3.36 Up = 9 kV,fbase = 9 kHz,fm = 800 Hz 56.23 3.78 Up = 9 kV,fbase = 11 kHz,fm = 1000 Hz 62.35 3.82 Up = 11 kV,fbase = 7 kHz,fm = 800 Hz 66.23 2.99 Up = 11 kV,fbase = 9 kHz,fm = 1000 Hz 70.51 3.64 Up = 11 kV,fbase = 11 kHz,fm = 200 Hz 66.16 2.81 表 6 NS–DBD模型测试电参数
Table 6 Electrical parameters of testing data for NS–DBD model
电压Up/kV 脉冲频率fp/Hz 5,7,9,11 300,500,700,900,1100 表 7 不同电参数下NS–DBD模型降噪前后均方根误差
Table 7 RMSE value of NS–DBD model under different testing electrical parameters
激励电参数 RMSE1 RMSE2 Up = 5 kV,fp = 300 Hz 40.36 4.36 Up = 5 kV,fp = 500 Hz 51.63 4.89 Up = 5 kV,fp = 700 Hz 62.22 4.78 Up = 7 kV,fp = 500 Hz 50.24 4.86 Up = 7 kV,fp = 700 Hz 59.33 4.88 Up = 7 kV,fp = 900 Hz 68.36 4.98 Up = 9 kV,fp = 700 Hz 66.32 4.48 Up = 9 kV,fp = 900 Hz 72.56 4.36 Up = 9 kV,fp = 1100 Hz 79.85 4.90 Up = 11 kV,fp = 300 Hz 68.49 4.22 Up = 11 kV,fp = 900 Hz 90.22 4.23 Up = 11 kV,fp = 1100 Hz 105.62 4.58 表 8 降噪后的压力信号均值与干净压力信号均值对比
Table 8 Mean value comparison between the denoised pressure signal and the clean pressure signal
激励电参数 降噪后信号与
真实信号的
均值差/PaAC–DBD Up = 5 kV,fbase = 6 kHz,fm = 200 Hz 1.26 Up = 5 kV,fbase = 8 kHz,fm = 400 Hz 1.15 Up = 7 kV,fbase = 6 kHz,fm = 400 Hz 1.36 Up = 7 kV,fbase = 8 kHz,fm = 600 Hz 1.44 Up = 9 kV,fbase = 6 kHz,fm = 600 Hz 1.52 Up = 9 kV,fbase = 8 kHz,fm = 800 Hz 1.21 Up = 11 kV,fbase = 6 kHz, fm = 800 Hz 1.58 Up = 11 kV,fbase = 8 kHz, fm = 1000 Hz 1.61 NS–DBD Up = 6 kV,fp = 200 Hz 2.98 Up = 7 kV,fp = 300 Hz 2.32 Up = 8 kV,fp = 400 Hz 2.36 Up = 9 kV,fp = 500 Hz 2.22 Up = 10 kV,fp = 600 Hz 2.43 Up = 11 kV,fp = 700 Hz 2.58 Up = 13 kV,fp = 800 Hz 2.46 Up = 14 kV,fp = 900 Hz 2.77 -
[1] 李应红, 吴云. 等离子体激励调控流动与燃烧的研究进展与展望[J]. 中国科学(技术科学), 2020, 50(10): 1252–1273. DOI: 10.1360/SST-2020-0111 LI Y H, WU Y. Research progress and outlook of flow control and combustion control using plasma actuation[J]. Scientia Sinica (Technologica), 2020, 50(10): 1252–1273. doi: 10.1360/SST-2020-0111
[2] 赵志杰, 罗振兵, 刘杰夫, 等. 基于分布式合成双射流的飞行器无舵面三轴姿态控制飞行试验[J]. 力学学报, 2022, 54(5): 1220–1228. DOI: 10.6052/0459-1879-21-586 ZHAO Z J, LUO Z B, LIU J F, et al. Flight test of aircraft three-axis attitude control without rudders based on distributed dual synthetic jets[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(5): 1220–1228. doi: 10.6052/0459-1879-21-586
[3] 姚张奕, 史志伟, 董益章. 深度强化学习在翼型分离流动控制中的应用[J]. 实验流体力学, 2022, 36(3): 55–64. DOI: 10.11729/syltlx20210085 YAO Z Y, SHI Z W, DONG Y Z. Deep reinforcement learning for the control of airfoil flow separation[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(3): 55–64. doi: 10.11729/syltlx20210085
[4] 兰子奇, 史志伟, 孙琪杰, 等. AC–DBD等离子体激励对L形截面钝体风荷载减阻的实验研究[J]. 实验流体力学, 2021, 35(2): 83–91. DOI: 10.11729/syltlx20200095 LAN Z Q, SHI Z W, SUN Q J, et al. Experimental study on drag reduction of L-shaped bluff body by AC–DBD plasma actuation[J]. Journal of Experiments in Fluid Mechanics, 2021, 35(2): 83–91. doi: 10.11729/syltlx20200095
[5] CHENG X Q, WONG C W, HUSSAIN F, et al. Flat plate drag reduction using plasma-generated streamwise vortices[J]. Journal of Fluid Mechanics, 2021, 918: A24. doi: 10.1017/jfm.2021.311
[6] DUONG A H, CORKE T C, THOMAS F O. Characteristics of drag-reduced turbulent boundary layers with pulsed-direct-current plasma actuation[J]. Journal of Fluid Mechanics, 2021, 915: A113. doi: 10.1017/jfm.2021.167
[7] LI Z, SHI Z W, DU H, et al. Analysis of flow separation control using nanosecond-pulse discharge plasma actuators on a flying wing[J]. Plasma Science and Technology, 2018, 20(11): 116–125.
[8] 周岩, 罗振兵, 王林, 等. 等离子体合成射流激励器及其流动控制技术研究进展[J]. 航空学报, 2022, 43(3): 90–132. DOI: 10.7498/aps.68.20190683 ZHOU Y, LUO Z B, WANG L, et al. Plasma synthetic jet actuator for flow control: review[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(3): 90–132. doi: 10.7498/aps.68.20190683
[9] WU B, GAO C, LIU F, et al. Reduction of turbulent boundary layer drag through dielectric-barrier-discharge plasma actuation based on the Spalding formula[J]. Plasma Science and Technology, 2019, 21(4): 107–114.
[10] 金元中, 郑博睿, 喻明浩, 等. 滑动放电等离子体控制细长体头部背风区非对称涡实验研究[J]. 实验流体力学, 2022, 36(5): 43–51. DOI: 10.11729/syltlx20210101 JIN Y Z, ZHENG B R, YU M H, et al. Experimental study on flow control of asymmetric vortex over the leeward region of the head of the slender body by sliding discharge plasma actuation[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(5): 43–51. doi: 10.11729/syltlx20210101
[11] 张卫国, 史喆羽, 李国强, 等. 风力机翼型动态失速等离子体流动控制数值研究[J]. 力学学报, 2020, 52(6): 1678–1689. DOI: 10.6052/0459-1879-20-090 ZHANG W G, SHI Z Y, LI G Q, et al. Numerical study on dynamic stall flow control for wind turbine airfoil using plasma actuator[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1678–1689. doi: 10.6052/0459-1879-20-090
[12] 黄广靖, 戴玉婷, 杨超. 低雷诺数俯仰振荡翼型等离子体流动控制[J]. 力学学报, 2021, 53(1): 136–155. DOI: 10.6052/0459-1879-20-183 HUANG G J, DAI Y T, YANG C. Plasma-based flow control on pitching airfoil at low Reynolds number[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 136–155. doi: 10.6052/0459-1879-20-183
[13] 梁华, 李应红, 程邦勤, 等. 等离子体气动激励抑制翼型失速分离的仿真研究[J]. 航空动力学报, 2008, 23(5): 777–783. DOI: 10.13224/j.cnki.jasp.2008.05.004 LIANG H, LI Y H, CHENG B Q, et al. Numerical simulation on airfoil stall separation suppression by plasma aerodynamic actuation[J]. Journal of Aerospace Power, 2008, 23(5): 777–783. doi: 10.13224/j.cnki.jasp.2008.05.004
[14] 杜海, 史志伟, 程克明, 等. 纳秒脉冲等离子体分离流控制频率优化及涡运动过程分析[J]. 航空学报, 2016, 37(7): 2102–2111. DU H, SHI Z W, CHENG K M, et al. Frequency optimization and vortex dynamic process analysis of separated flow control by nanosecond pulsed plasma discharge[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2102–2111.
[15] 郝琳召, 张彬乾, 陈真利. 纳秒等离子体激励控制翼型流动分离机理研究[J]. 航空工程进展, 2014, 5(1): 25–32. DOI: 10.3969/j.issn.1674-8190.2014.01.005 HAO L Z, ZHANG B Q, CHEN Z L. Investigation on mechanisms of separation control over an airfoil using nanosecond pulsed plasma actuator[J]. Advances in Aeronautical Science and Engineering, 2014, 5(1): 25–32. doi: 10.3969/j.issn.1674-8190.2014.01.005
[16] MENG X S, LONG Y X, WANG J L, et al. Dynamics and control of the vortex flow behind a slender conical forebody by a pair of plasma actuators[J]. Physics of Fluids, 2018, 30(2): 024101. doi: 10.1063/1.5005514
[17] 孟宣市, 惠伟伟, 易贤, 等. AC–SDBD等离子体激励防/除冰研究现状与展望[J]. 空气动力学学报, 2022, 40(2): 31–49. DOI: 10.7638/kqdlxxb-2021.0159 MENG X S, HUI W W, YI X, et al. Anti-/ De-icing by AC–SDBD plasma actuators: status and outlook[J]. Acta Aerodynamica Sinica, 2022, 40(2): 31–49. doi: 10.7638/kqdlxxb-2021.0159
[18] CAI J S, TIAN Y Q, MENG X S, et al. An experimental study of icing control using DBD plasma actuator[J]. Experiments in Fluids, 2017, 58(8): 102. doi: 10.1007/s00348-017-2378-y
[19] WEI B, WU Y, LIANG H, et al. SDBD based plasma anti-icing: A stream-wise plasma heat knife configuration and criteria energy analysis[J]. International Journal of Heat and Mass Transfer, 2019, 138: 163–172. doi: 10.1016/j.ijheatmasstransfer.2019.04.051
[20] LATTARI F, GONZALEZ LEON B, ASARO F, et al. Deep learning for SAR image despeckling[J]. Remote Sensing, 2019, 11(13): 1532. doi: 10.3390/rs11131532
[21] ZHU W Q, MOUSAVI S M, BEROZA G C. Seismic signal denoising and decomposition using deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9476–9488. doi: 10.1109/TGRS.2019.2926772
[22] TIAN C W, FEI L K, ZHENG W X, et al. Deep learning on image denoising: an overview[J]. Neural Networks, 2020, 131: 251–275. doi: 10.1016/j.neunet.2020.07.025
[23] GOYAL B, DOGRA A, AGRAWAL S, et al. Image denoising review: from classical to state-of-the-art approaches[J]. Information Fusion, 2020, 55: 220–244. doi: 10.1016/j.inffus.2019.09.003
[24] ANWAR S, BARNES N. Real image denoising with feature attention[C]//Proc of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE, 2020: 3155-3164.






 下载:
下载: