Experimental study on generation of non-Newtonian droplets in dripping mode in a flow focusing microchannel
-
摘要: 液滴微流控是微流控领域重要分支，其所涉及的生物流体往往具有非牛顿性质。为深入理解非牛顿性质对液滴生成的影响，配置4种不同流变特性的流体，系统研究流动聚焦微通道中滴流模式下的非牛顿液滴生成。结果表明：与牛顿液滴相比，非牛顿液滴生成表现出更显著的“连珠现象”；不同非牛顿性质对液滴生成的影响截然不同，剪切稀化和弹性效应对液滴尺寸和生成频率的作用相反。液柱颈缩动力学结果显示：单一的剪切稀化效应使得非牛顿液滴液柱颈缩过程与牛顿液滴相似，均只有流动驱动阶段；单一的弹性效应则使得非牛顿液滴液柱颈缩后期出现不同于牛顿流体的毛细驱动阶段；而剪切稀化和弹性效应的共同作用会导致液柱颈缩过程中更显著的毛细驱动阶段和液柱断裂后更显著的“连珠现象”。Abstract: Droplet microfluidic is an important branch of the microfluidic field and the biological fluids involved in it often have non-Newtonian properties. In order to understand the influence of non-Newtonian properties on droplet formation, four kinds of fluids with different rheological properties were configured to systematically study the non-Newtonian droplet formation in the dripping mode in a flow focusing microchannel. The results show that compared with Newtonian droplet formation, non-Newtonian droplet formation shows a more significant “beads-on-a-string” phenomenon. Different non-Newtonian properties have different effects on droplet formation. Shear thinning effect and elastic effect have opposite effects on the droplet size and formation frequency. The results of liquid column necking dynamics show that the process of liquid column necking is similar to that of Newtonian fluid due to a single shear thinning effect. The single elastic effect makes the capillary drive stage which appears of liquid column necking different from that of Newtonian fluid. The combined effect of the elastic effect and shear thinning effect leads to more significant capillary drive stage in the process of column necking and more significant “beads-on-a-string” after column necking.
-
0 引 言
液滴微流控技术是近20年间发展起来的一种操纵微小体积液体的全新技术。液滴可为化学、生物、医学及材料科学领域研究和应用提供孤立的微尺度隔间，避免交叉污染，可在很大程度上减少昂贵试剂消耗[1-6]。基于传统搅拌方式制备的液滴单分散性极差、形状不规则，不利于后续定量分析与检测。微流控技术可解决上述问题，制备的液滴通常尺寸均一，在建立均匀微环境、精确添加药物成分和化学反应物剂量等方面具有独特优势[7-10]。
典型的微流控液滴生成结构有交叉流动、同轴流动和流动聚焦[11-12]。相较于另外2种结构，流动聚焦结构不仅可以更稳定地生成大小均一、空间分布均匀的液滴，还可以更灵活地控制液滴的尺寸[13-16]，故而获得更多关注。2种互不相溶的液体从不同的侧通道流入同一主通道，连续相在离散相的外围流动，挤压和拉伸中间离散相流体，离散相液柱最终断裂成液滴[12]。随着两相流量比的增大，液滴的生成模式会由滴流向射流转变。与射流模式相比，滴流模式下的液滴生成更加稳定[17-19]。在滴流模式下，离散相进入交叉部位，在流动剪切作用下破碎成液滴。受壁面影响，离散相在交叉部位的挤压过程是准静态的，界面时刻保持能量最小，从而生成稳定可控、单分散性液滴[11]。
基于简单牛顿流体的微流控液滴生成已有广泛研究，但涉及非牛顿流体液滴生成的研究还相对较少。非牛顿流体即不满足剪应力与剪切应变率线性相关关系的流体，如血液、黏液、高分子水溶液等，在自然界和工业中广泛存在。诸多重要应用中如药物合成、细胞封装、药物筛选和递送等所使用的流动介质往往是非牛顿流体[13, 20]。近年来，流动聚焦微通道中非牛顿流体性质对液滴生成的影响受到了广泛关注[21-23]。根据离散相和连续相性质的不同，非牛顿液滴生成可分为2种情形：连续相为非牛顿流体和离散相为非牛顿流体。Arratia等[24]研究了当离散相为非牛顿流体时液滴生成的断裂动力学，发现弹性和剪切稀化等非牛顿特性会使液滴生成过程变得复杂。Derzsi等[25]研究了连续相的弹性对液滴产生的影响，指出调整连续相和离散相黏度比可以提高液滴单分散性并减小液滴尺寸。任勇等[26]研究了连续相的剪切稀化特性和弹性对液滴生成的影响，发现剪切稀化会导致更大的液滴尺寸和更快的破碎过程；弹性则会加剧牛顿流体液滴的变形。付涛涛等[15]研究发现流动聚焦装置中剪切稀化流体形成液滴的破碎过程分为可控挤压阶段和快速夹断阶段；并总结阶段过渡规律，基于流动聚焦装置提出剪切稀化流体形成液滴尺寸的一般标度规律。需要指出的是：现有研究普遍关注单一弹性、剪切稀化等非牛顿特性对液滴尺寸的影响[25, 27-28]，不同非牛顿特性对液滴生成的具体影响还不明确，单一及协同效应对液滴生成尺寸、频率和液柱颈缩（necking）动力学过程的影响还缺乏系统的认识[24, 29]。
基于以上论述，本文旨在探索流动聚焦微通道中滴流模式下，不同非牛顿性质对液滴生成的影响。首先，与牛顿液滴对比，揭示非牛顿液滴生成的主要特征，并简要分析液滴尺寸、生成频率随流量比的变化；然后，分析剪切稀化和弹性单一/协同作用对液滴生成的宏观影响，发展液滴尺寸和生成频率的标度率公式；最后，表征非牛顿液滴液柱颈缩动力学过程并划分典型阶段，探讨非牛顿性质影响液滴生成的微观机制。本文围绕流动聚焦微通道、滴流模式和非牛顿流体性质展开液滴生成的系统研究，不仅可以扩展对液滴微流控基础理论的认知，还可为非牛顿液滴的实际应用提供一定参考。
1 材料和方法
1.1 流体配置
实验选取橄榄油作为连续相流体，其密度和黏度分别为0.92 g/cm3和78 mPa·s；选取3种聚合物溶液作为离散相流体，分别为聚环氧乙烷水溶液（Polyethylene Oxide, PEO, 0.4 wt.%），聚乙烯吡咯烷酮水溶液（Polyvinyl Pyrrolidone, PVP, 2 wt.%），黄原胶水溶液（Xanthan Gum, XG, 0.01 wt.%）。离散相的牛顿流体对比项选用甘油–水混合液（Glycerin–Water, GW, 60 wt.%）。所使用聚合物均购买自西格玛–奥德里奇公司，配置时未做其他处理。聚合物溶液采用回旋振荡器以100 r/min的速率混合1～2天；甘油–水混合液直接按照配比质量分数加入去离子水，充分摇混即可。所有配制溶液均静置6 h以上再进行后续实验。
流体流变性质采用锥板旋转流变仪测量（Physica MCR302, Anton Paar GmbH），所用锥板直径为50 mm，锥角为0.3 rad。在剪切率
$ \dot \gamma $ =1～103 s–1范围内测量了流体黏度η（图1（a）），在恒应变为4%的动态振荡实验中，测量得到复剪切模量G*随角频率ω的变化（图1（b））。如图1所示，GW溶液的黏度一直保持恒定，是典型的牛顿流体；PVP溶液的黏度在所测剪切率范围内保持恒定，无剪切稀化特性，但具有显著弹性；XG溶液的黏度在所测剪切率范围内持续降低，表现为显著的剪切稀化特性；PEO溶液在较高剪切率水平时具有明显的剪切稀化特性，并兼具一定弹性特性；同时，所选用的4种离散相流体在低剪切率下黏度近似相等。由于XG溶液与PEO溶液剪切稀化形式不同，因此分别采用Carreau–Yasuda模型[30]和改进的Carreau模型[31]对所测XG溶液和PEO溶液的黏度数据进行拟合：
$$ \frac{{\eta{{\left( {{{\dot \gamma }}} \right)}_{{\rm{XG}}}} - {\eta _{{0}}}}}{{{\eta _0} - {\eta _\infty }}} = \frac{1}{{{{[1 + {{（{\lambda _{\rm{C}}} \cdot {{\dot \gamma }}）}^{{a}}}]}^{{{{n}} \mathord{\left/ {\vphantom {{{n}} {{a}}}} \right. } {{a}}}}}}} $$ (1) $$ \frac{{\eta{{\left( {{{\dot \gamma }}} \right)}_{{\rm{PEO}}}}}}{{{\eta _{{0}}}}}{{ = }}\frac{1}{{{{[1 + {{（{\lambda _{\rm{C}}} \cdot {{\dot \gamma }}）}^{{a}}}]}^{{{{n}} \mathord{\left/ {\vphantom {{{n}} {{a}}}} \right. } {{a}}}}}}} $$ (2) 式中：
${\eta_{}}（{{\dot \gamma }}）$ 为剪切黏度，$ {\eta _{\text{0}}} $ 和$ {\eta _\infty } $ 分别为零剪切黏度和无限剪切黏度；$ {\lambda _{\rm{C}}} $ 为流体的特征时间，对应$ {\text{η }} $ 开始减小的临界剪切率${{\dot \gamma }}$ ；n和a分别为幂律指数和Yasuda等[30]引入的拟合参数。整体拟合参数如表1所示。表 1 Carreau-Yasuda模型和改进Carreau模型的拟合系数Table 1 The fitting parameters of the Carreau-Yasuda model and modified Carreau model流体 ${\eta _0 }/({\rm{Pa} } \cdot {\rm{s} } )$ ${\eta _\infty }/({\rm{Pa} } \cdot {\rm{s} })$ ${\lambda _{\rm{C}}}/{\rm{ms}}$ a n XG 0.0187 0.00182 0.27 2 0.03 PEO 0.0106 0.00462 0.02 1.1 0.22 液–液界面张力在液柱颈缩和断裂过程中起着重要作用。实验使用界面张力仪（OSA200–B, 宁波新边界仪器有限公司），在橄榄油内采用悬滴法测量了不同非牛顿流体与橄榄油之间的界面张力（表2），对摄像机进行180°旋转得到以下如图2所示的结果。
表 2 不同溶液与橄榄油之间的界面张力Table 2 Interfacial tension between different solutions and olive oil流体 密度ρ/（g·cm−3） 界面张力$ \sigma $/（mN·m−1） GW 1.158 20.49±0.16 PVP 1.020 18.22±0.17 XG 1.001 21.54±0.28 PEO 1.004 18.22±0.23 1.2 芯片加工
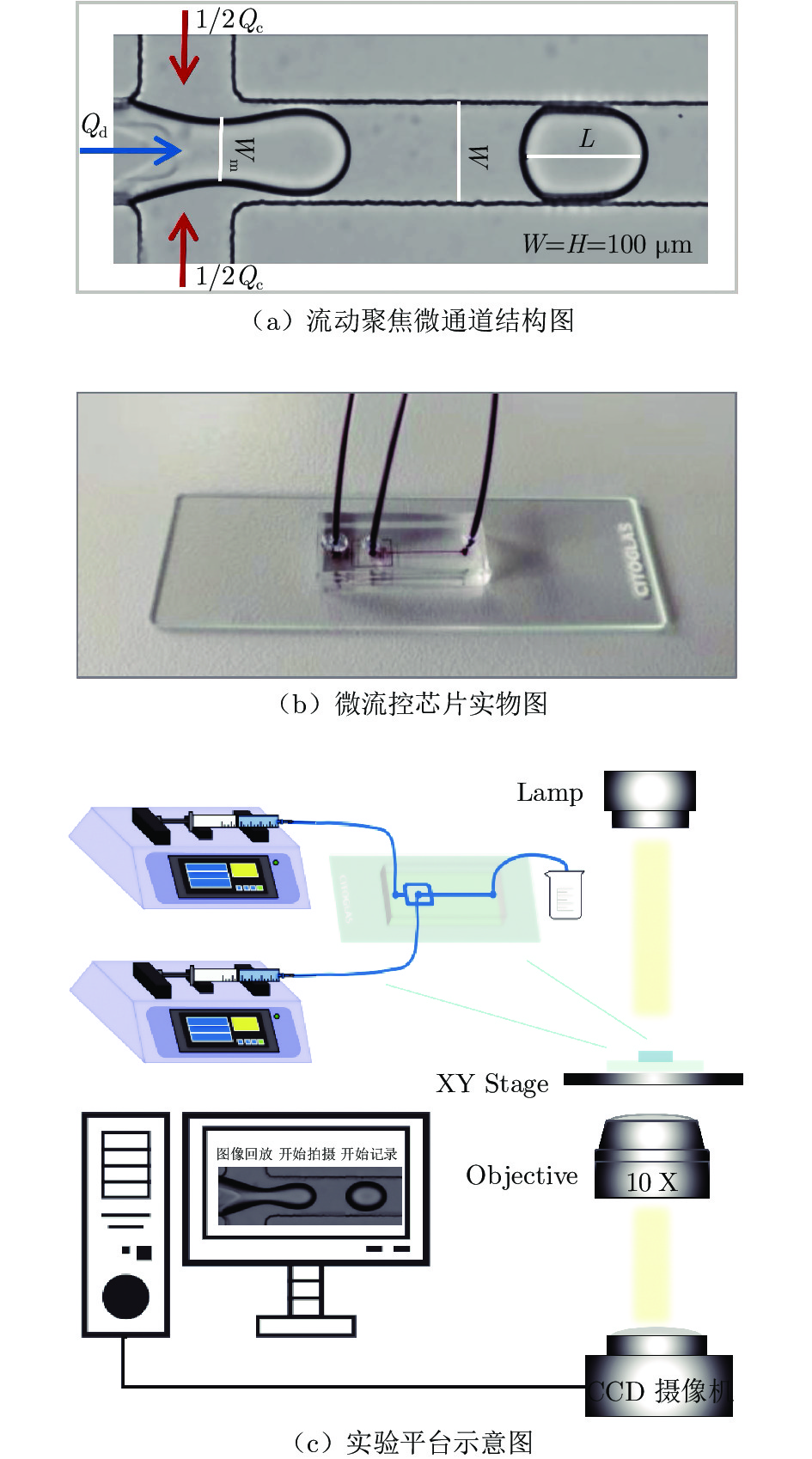
图3（a）为本研究所用流动聚焦微通道的结构，微通道宽度（W）、深度（H）和结构中其他开口均为100 μm。图中Wm为液柱纵向最小距离，L为液滴尺寸。滴流模态下的液滴生成会产生比通道宽度大很多的液滴，因此使用主通道方向液滴长度来表征液滴尺寸。采用矩形结构以尽可能地减少壁面对液滴生成的影响，基于二维图像合理分析液滴生成过程[19]。为简化连续相输入控制，将两侧连续相通道在外侧合并成一个主入口。主入口连续相和离散相的流量分别用Qc和Qd表示，即连续相两侧通道流量分别为1/2Qc。
图3（b）为微流控芯片实物。芯片是基于标准软光刻技术，采用聚二甲基硅氧烷（Polydimethylsiloxane, PDMS）制备的：首先，根据芯片结构在硅板上加工SU8–3050掩模（苏州中芯启恒科学仪器有限公司）；其次，将PDMS与固化剂按10∶1的比例搅拌均匀；然后，将其在真空容器中首次脱气并在掩模上浇铸，在真空容器中进行二次脱气后放入干燥箱中（70 ℃，2 h）；最后，将PDMS模块剥离掩模，在出、入口处打孔和插管，经由等离子清洗机处理（PC–6S，嘉润万丰（北京）科技有限公司）后，完成PDMS与盖玻片（25 mm × 75 mm）的键合。为减少壁面对液滴生成的影响，将键合后的芯片放置于干燥箱中（80 ℃，12 h），保证PDMS表面恢复到原本的疏水特性。
1.3 实验操作及数据处理
图3（c）为实验平台示意图。实验采用高精度流量泵（Pump 11 Elite, Harvard Apparatus Inc.）驱动2个1mL注射器（BD, Becton Dickinson Inc.）将流体以恒定流量通入微通道中。通过倒置显微镜（Olympus IX73, Olympus lnc.）观察液滴生成现象，使用高速CCD摄像机（CP70–1–M–1000，湖南科天健光电技术有限公司）以2000 帧/s的速度进行记录。本实验中，控制q=Qc/Qd=5～25、Qc=25～625 μL/h、Qd=5～25 μL/h，所有实验均在室温下进行。
使用ImageJ软件和MATLAB自编程序处理实验图像：使用ImageJ提取单个液滴生成周期后，测量液滴尺寸和频率；使用MATLAB自编程根据灰度值分布提取液滴轮廓，对液滴生成全过程的油–水界面轮廓进行捕捉，提取液滴生成液柱颈缩过程中液柱最小宽度随时间的变化过程。同一工况选取5个以上液滴生成周期进行测量，取平均值并考虑误差。
2 结果和讨论
2.1 非牛顿液滴生成的典型特征
在流动聚焦微通道中通入连续相和离散相流体后，两相界面张力不足以维持连续相施加给离散相的流动剪切力时，离散相在交叉结构处被连续相挤压形成宽度均匀的液柱，在界面张力和黏性力共同作用下进一步颈缩，最终断裂形成液滴。为便于分析液滴生成过程，将液柱即将发生颈缩的时刻定义为初始时刻（t=0），并定义液柱颈缩至最细但未断开的时刻为断裂时间tb。图4为GW、PVP、XG、PEO 4种离散相流体在Qd=20 μL/h、q=20流量条件下的液滴生成过程，对应的断裂时间分别为15.0、16.5、13.5和25 ms
![]()
图 4 滴流模式下4种离散相液滴生成过程实验图像Fig. 4 Experimental images of droplet formation process of four dispersed phases in dripping mode从图4可以看出，作为典型的牛顿流体，GW液柱颈缩后，液柱与液滴相连，液滴生成后液柱被下一个液滴回收或收缩为一个极小的卫星液滴。在液滴生成初期（t/tb ≤ 0.4），3种非牛顿流体液柱颈缩现象与牛顿流体相似，通过观察相同无量纲时间段内液柱纵向最小距离Wm变化，发现其颈缩速率也相近；而在液滴生成后期（t/tb ≥ 0.8），非牛顿液滴颈缩过程与牛顿液滴明显不同，非牛顿液滴形成的液柱比牛顿液滴明显更长，且液柱最终会演化为多个相连的卫星液滴。这种更长的液柱和液柱断裂后的连珠现象（beads-on-a-string）是非牛顿液滴生成的典型特征[32-33]。
此外，在相同的流量条件下，不同非牛顿液滴生成的液滴尺寸、液柱长度和卫星液滴连珠现象亦有一定差异。与PVP溶液和PEO溶液相比，XG溶液的液滴尺寸更大一些；与PVP溶液和XG溶液相比，PEO溶液的液柱更长，且连珠现象更明显。后文将就这两方面开展具体分析。
2.2 液滴尺寸和生成频率
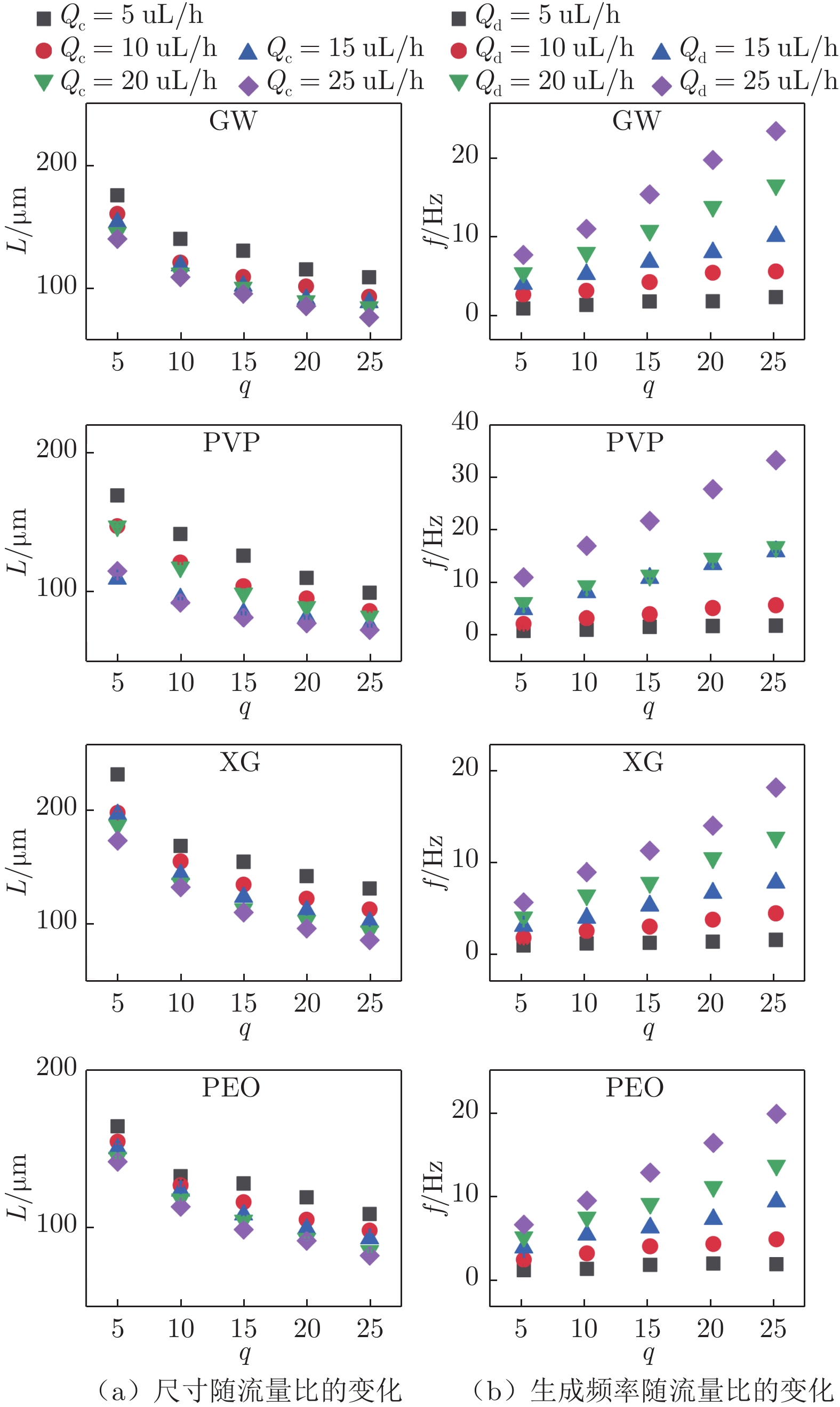
图5（a）为不同离散相流量下， GW、PVP、XG 和PEO液滴尺寸随流量比的变化情况。可以看出：4种液滴尺寸均表现出一致的变化规律。在流量比固定的情况下，液滴尺寸随着离散相流量的增大而减小；在离散相流量固定的情况下，液滴尺寸随着流量比的增大而减小，即随着连续相流量的增大而减小。图5（b）则相应地展示了不同离散相流量下，4种液滴生成频率f随流量比q的变化情况。可以看出：4种液滴的生成频率亦表现出一致的变化规律，即液滴生成频率随离散相流量和流量比增大而增大。上述规律与已有文献研究结果一致[34-35]。
![]()
图 5 液滴尺寸和液滴生成频率随流量比的变化Fig. 5 Droplet size and the frequency of droplet generation vary with the flow ratio与图4所示一致，流动条件相同时，3种非牛顿流体的液滴尺寸和生成频率均存在差异。这种差异反映了弹性和剪切稀化特性的单独/协同影响。实际上，本研究选用的PVP，XG和PEO溶液不仅具有与GW溶液相近的剪切黏度，还分别表现为显著弹性（无剪切稀化）、显著剪切稀化特性（微弱弹性）和兼具一定弹性和剪切稀化特性（图1）。为探究弹性和剪切稀化对液滴尺寸和生成频率的影响，绘制了3种非牛顿液滴与牛顿液滴相对尺寸（
$L/L_{{\rm{max}},{\rm{G}}} $ ）和相对生成频率（$f/f_{{\rm{min}},{\rm{G}}} $ ）随流量比变化的对比图（图6），其中，$L_{{\rm{max}},{\rm{G}}}$ 和$f_{{\rm{min}},{\rm{G}}} $ 分别为相同离散相流量条件下GW液滴的最大尺寸和最小生成频率。![]()
图 6 4种离散相生成液滴的相对尺寸和相对生成频率随流量比的变化Fig. 6 Relative droplet size and relative frequency vary with the flow ratio of the four dispersed phases图6（a）展示了弹性和剪切稀化特性对液滴相对尺寸的影响，即剪切稀化特性导致液滴相对尺寸增大，而弹性则使得液滴相对尺寸减小。可以从两方面进行解释：一方面，XG溶液具有强烈的剪切稀化特性，在相同剪切率下，其黏度远低于牛顿对比相GW，离散相流体流动所受的黏性阻力更小，导致生成的液滴相对尺寸增大[28, 36]；另一方面，虽然与GW溶液的黏度曲线保持一致，但PVP溶液显著的弹性会使流动受到额外的弹性阻力，从而使液滴相对尺寸更小[27, 37]，由于PEO溶液兼具弹性和剪切稀化特性，使得生成的液滴相对尺寸介于XG溶液（显著剪切稀化特性）和PVP溶液（显著弹性）之间，从而表现出与牛顿流体GW溶液相似的变化。图6（b）展示了弹性和剪切稀化特性对液滴相对生成频率的影响。可以看出：与对液滴相对尺寸的影响规律相反，剪切稀化特性会导致液滴相对生成频率下降，弹性则使得液滴相对生成频率提高。
进一步，通过拟合实验数据，得到该实验条件下液滴尺寸和生成频率的标度律公式：
$$ {{L}}/{{{L}}_{\max,{{\rm{G}}}}} \propto {{A}} + {{B}}{{q + {{C}}}}{{{q}}^2} $$ (3) $$ {{f}}/{{{f}}_{\min,{{\rm{G}}}}} \propto {{D}} + {{E}}{{q}} $$ (4) 式中：A、B、C、D和E为拟合系数，与流体性质和通道因素相关。图6中虚线为拟合曲线，拟合系数如表3所示。从数据中也可以看出：XG溶液的剪切稀化特性使得液滴相对尺寸增大，相对生成频率减小；PVP溶液的弹性使得液滴相对尺寸减小，相对生成频率增大；PEO溶液同时具有弹性与剪切稀化特性，从而表现出与GW相似的相对尺寸和相对生成频率。
表 3 不同离散相液滴的拟合系数Table 3 Fitting coefficients of droplets of different dispersed phases拟合系数 液滴 GW PVP XG PEO A 1.21±0.02 1.01±0.09 1.48±0.08 1.19±0.04 B −0.05±0.01 −0.04±0.01 −0.07±0.01 −0.05±0.01 C 1.10×10−3 7.00×10−4 1.37×10−3 1.20×10−3 D 0.44±0.01 0.63±0.19 0.2±0.09 0.55±0.03 E 0.11±0.01 0.14±0.01 0.08±0.01 0.06±0.01 2.3 液滴生成的液柱颈缩动力学
上一节分析了非牛顿性质对液滴尺寸和生成频率的影响，下面将进一步探究非牛顿液滴生成时的液柱颈缩动力学。为定量表征液柱颈缩过程，定义液柱纵向最小距离为Wm（见图3（a）），探究Wm随时间t的变化情况。图7（a）和（b）分别为4种离散相流体在离散相流量Qd相同和流量比q相同时Wm随时间的变化曲线。可以看出：不同流体液滴的液柱颈缩过程有显著差异。XG溶液具有与牛顿流体极为相似的颈缩过程，而PVP溶液与PEO溶液在颈缩后期则表现出与牛顿流体完全不同的颈缩过程。这可以从两方面来解释：一方面，剪切稀化效应使得流体具有较小的黏性阻力，从而导致液柱更快、更容易断裂；另一方面，弹性效应的存在使得液滴颈缩过程中要克服弹性阻力，导致液柱在较长时间内维持极细的长丝状，从而减缓液柱颈缩过程。两种效应同时存在时，又会引起黏性力与弹性力之间的相互作用，从而导致PEO溶液与PVP溶液表现不同的颈缩特征。
![]()
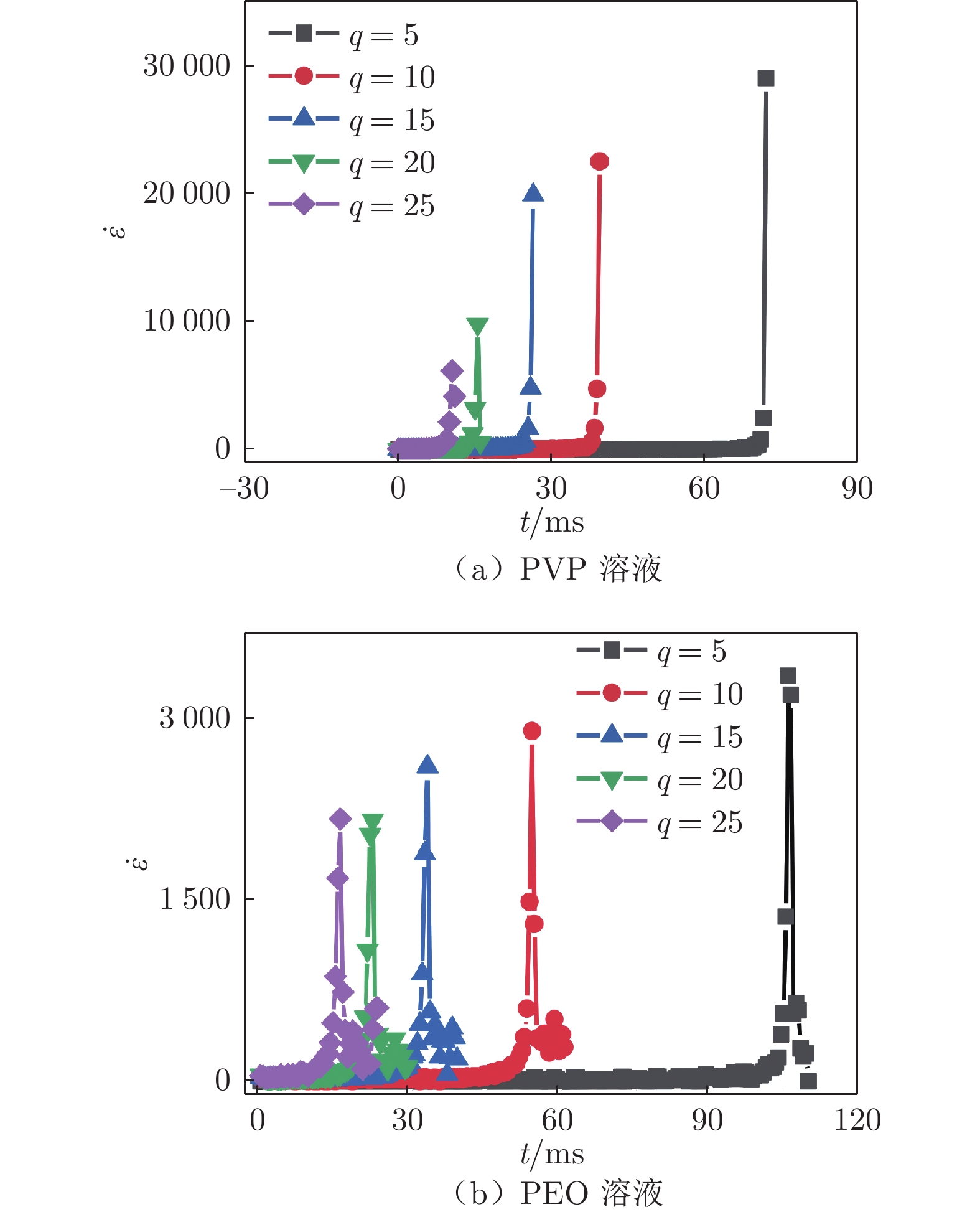
图 7 4种液滴生成时液柱颈缩过程图Fig. 7 Diagram of liquid column necking process during the formation of four droplets非牛顿液滴液柱颈缩过程可以根据过渡时间（transition time, tp）分为两个阶段。可通过对比牛顿液滴液柱颈缩过程获取过渡时间tp，也可以通过拟合扩展延伸率随时间的变化提取[15, 24]。图8为在Qd=10 μL/h的流量条件下，PVP、PEO溶液的扩展延伸率
$\dot \varepsilon $ （式5）随时间的变化，扩展延伸率达到最大值所对应的时刻即为过渡时间tp。![]()
图 8 不同流量比下扩展延伸率随时间的变化Fig. 8 Extensional strain rate$\dot \varepsilon $ as functions of the elapsed time at different flow ratio$$ \dot \varepsilon = {\frac{2}{{{W}}_{\text{m}}}} \cdot \frac{{\rm{d}}{{{W}}_{\rm{m}}}}{{\rm{d}}{{t}}} $$ (5) 基于上述方法分别获取不同对应流量条件下的过渡时间，可将非牛顿液滴液柱颈缩过程分为流动驱动阶段和毛细驱动阶段。在液滴液柱颈缩初期（t<tp），液柱头推进并限制连续相流体的流动，导致上游的静水压力增加，增加的压力促使液柱快速缩颈，形成流动驱动状态。需要指出的是：在颈缩前期，液滴形变小，聚合物分子没有发生较大的拉伸，其弹性效应可以忽略，此时非牛顿流体的弹性效应与牛顿流体间的差异可忽略不计。此阶段液柱颈缩主要由离散相的黏性力和两相界面的表面张力控制。因此，非牛顿流体表现出与具有相同剪切黏度的牛顿流体相似的颈缩过程，均处于流动驱动状态。液柱纵向最小距离Wm与剩余时间（residual time, tp−t）呈现幂律关系，由幂律函数
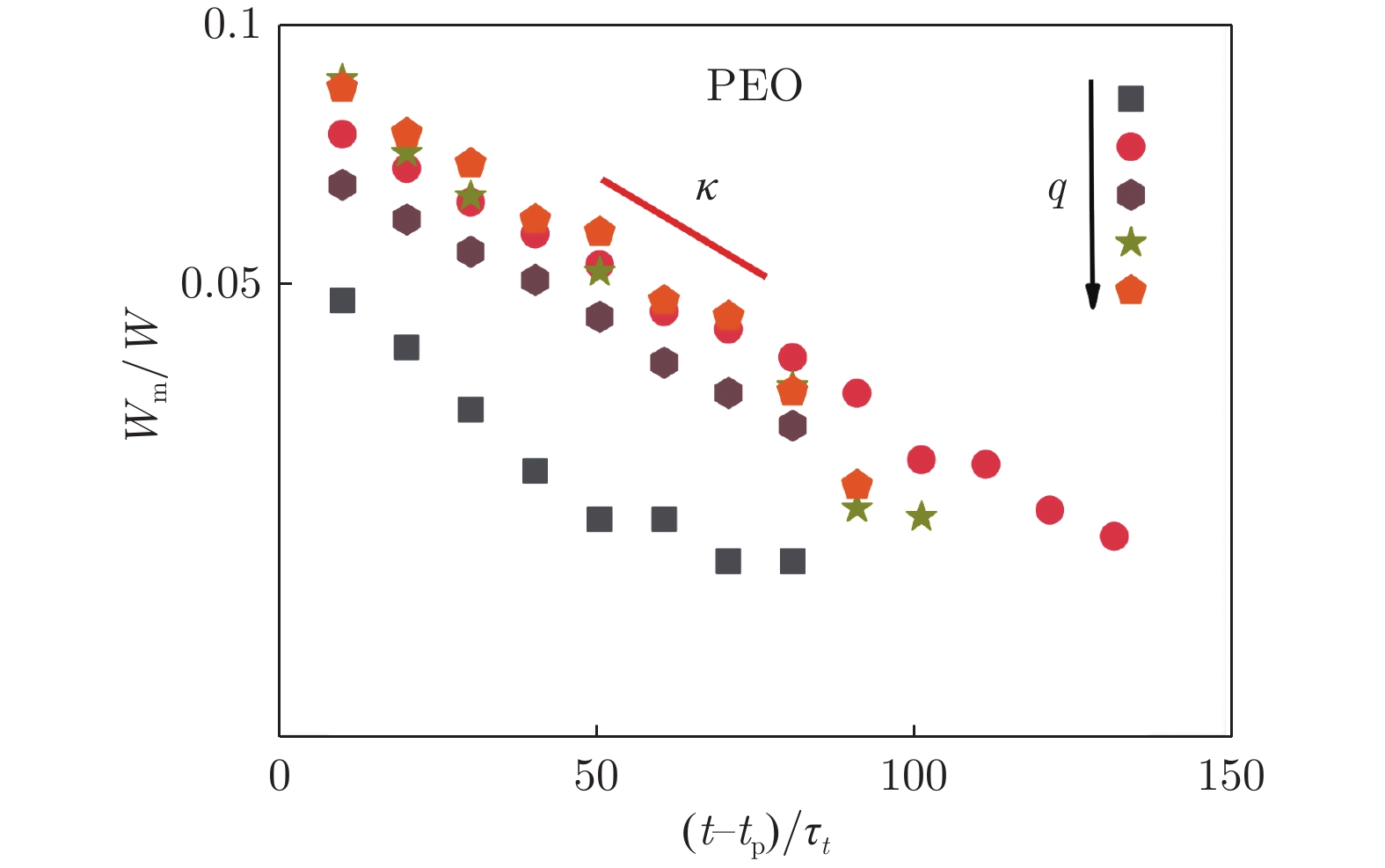
${{{W}}_{{{\rm{m}}}}}/{{{{W}}}} \propto {\left[ {{{\left( {{{{t}}_{\rm{p}}} - {{t}}} \right)} / {{{\tau} _{{t}}}}}} \right]^{\alpha} }$ 进行拟合，其中$\alpha $ 为幂律指数，${\tau _{{t}}} = {{{\eta }}_{\rm{d}}}({{\dot \gamma }}){{W}}/ {{\sigma }}$ [23, 35]，${{\rm{\eta }}_{\rm{d}}}({{\dot \gamma }})$ 为离散相黏度。图9为4种液滴在流动驱动阶段无量纲液柱纵向最小距离随无量纲剩余时间的变化。有趣的是：在本研究的通道结构和所有流量条件下，PVP溶液和PEO溶液$\alpha $ 值均约0.32，与牛顿流体的结果一致，表明弹性效应及界面张力微小差异对流动驱动阶段的影响基本可以忽略。而XG溶液$\alpha $ 值相对较大，表明XG溶液在流动驱动阶段颈缩速率快。这是由于XG溶液的强剪切稀化特性导致离散相黏度随着剪切速率增大而减小，从而使加速液滴破碎。![]()
图 9 无量纲最小距离Wm/W随无量纲剩余时间(tp–t)/τt的变化Fig. 9 Plots of the dimensionless minimum width Wm/W of the dispersed filament to the dimentionless residual time (tp–t)/τt在液滴液柱颈缩后期（t>tp），累积压力（accumulated pressure）在上游的分布随细丝延伸而变化，离散相受到连续相的挤压减小，拉伸力增大，非牛顿流体细丝细化速度变慢，液柱中的聚合物分子被高度拉伸，弹性效应开始发挥作用，具有弹性的PVP溶液和PEO溶液表现出与牛顿流体不同的颈缩阶段，即毛细驱动状态。此阶段的液柱颈缩主要由离散相的黏性力、弹性力和界面的表面张力控制。然而，PVP溶液的这一阶段并不明显。PVP溶液具有与GW溶液相似的黏度，且具有显著的弹性，但较高的黏度会阻碍聚合物分子的拉伸，使得溶液在颈缩后期也相对较快地被夹断，从而无法捕捉到较长的毛细驱动阶段。相比而言，PEO溶液同时具有剪切稀化特性和显著弹性，其内部聚合物分子因剪切稀化效应仅需克服较小的黏性力而在液柱内部得到充分拉伸，可以在较长时间内维持极细的液柱。Wm随偏移时间（shift time, t–tp）呈指数衰减，用指数函数
${{{W}}_{{{\rm{m}}}}}/{{W}} \propto \exp \left[ {{{\kappa }}\left( {{{t}} - {{{t}}_{\rm{p}}}} \right)/{\tau _{{t}}}} \right]$ 拟合，其中$ \kappa $ 为拟合系数，其数值取决于溶液性质，在当前实验中，$ \kappa $ 的取值为–0.0094±0.0001，拟合结果如图10所示。![]()
图 10 无量纲最小距离Wm/W随无量纲偏移时间(tp–t)/τt的变化Fig. 10 Plot of the dimensionless minimum width Wm/W of the dispersed filament to the dimensionless shift time (tp–t)/τt3 结 论
本研究选取4种不同流变特性的溶液为离散相、橄榄油为连续相，系统考察滴流模式下流动聚焦微通道中非牛顿液滴的生成，得到如下结论：
1）非牛顿液滴区别于牛顿液滴的主要特征是更长的液柱和液柱断裂后的连珠现象。
2）相同流动条件下，剪切稀化特性的作用是增大液滴尺寸、减小液滴生成频率，弹性则具有相反效果，二者同时存在会使得液滴尺寸与牛顿液滴相似。
3）液柱颈缩动力学结果表明：单一的剪切稀化效应使得非牛顿液滴液柱颈缩过程与牛顿液滴相似，均只有流动驱动阶段；单一的弹性效应则使得非牛顿液滴液柱颈缩后期出现不同于牛顿流体的毛细驱动阶段；而弹性效应和剪切稀化效应的共同作用会导致液柱颈缩过程中更显著的毛细驱动阶段和液柱断裂后更显著的“连珠现象”。
未来将考察不同程度的非牛顿性质对液滴生成的影响，以探究流体非牛顿性质对射流模式下液滴生成的影响，分析液滴内外流场及不稳定现象。
-
![]()
图 4 滴流模式下4种离散相液滴生成过程实验图像
Fig. 4 Experimental images of droplet formation process of four dispersed phases in dripping mode
![]()
图 5 液滴尺寸和液滴生成频率随流量比的变化
Fig. 5 Droplet size and the frequency of droplet generation vary with the flow ratio
![]()
图 6 4种离散相生成液滴的相对尺寸和相对生成频率随流量比的变化
Fig. 6 Relative droplet size and relative frequency vary with the flow ratio of the four dispersed phases
![]()
图 7 4种液滴生成时液柱颈缩过程图
Fig. 7 Diagram of liquid column necking process during the formation of four droplets
![]()
图 8 不同流量比下扩展延伸率随时间的变化
Fig. 8 Extensional strain rate
$\dot \varepsilon $ as functions of the elapsed time at different flow ratio![]()
图 9 无量纲最小距离Wm/W随无量纲剩余时间(tp–t)/τt的变化
Fig. 9 Plots of the dimensionless minimum width Wm/W of the dispersed filament to the dimentionless residual time (tp–t)/τt
![]()
图 10 无量纲最小距离Wm/W随无量纲偏移时间(tp–t)/τt的变化
Fig. 10 Plot of the dimensionless minimum width Wm/W of the dispersed filament to the dimensionless shift time (tp–t)/τt
表 1 Carreau-Yasuda模型和改进Carreau模型的拟合系数
Table 1 The fitting parameters of the Carreau-Yasuda model and modified Carreau model
流体 ${\eta _0 }/({\rm{Pa} } \cdot {\rm{s} } )$ ${\eta _\infty }/({\rm{Pa} } \cdot {\rm{s} })$ ${\lambda _{\rm{C}}}/{\rm{ms}}$ a n XG 0.0187 0.00182 0.27 2 0.03 PEO 0.0106 0.00462 0.02 1.1 0.22 
下载: 导出CSV
表 2 不同溶液与橄榄油之间的界面张力
Table 2 Interfacial tension between different solutions and olive oil
流体 密度ρ/（g·cm−3） 界面张力$ \sigma $/（mN·m−1） GW 1.158 20.49±0.16 PVP 1.020 18.22±0.17 XG 1.001 21.54±0.28 PEO 1.004 18.22±0.23
下载: 导出CSV
表 3 不同离散相液滴的拟合系数
Table 3 Fitting coefficients of droplets of different dispersed phases
拟合系数 液滴 GW PVP XG PEO A 1.21±0.02 1.01±0.09 1.48±0.08 1.19±0.04 B −0.05±0.01 −0.04±0.01 −0.07±0.01 −0.05±0.01 C 1.10×10−3 7.00×10−4 1.37×10−3 1.20×10−3 D 0.44±0.01 0.63±0.19 0.2±0.09 0.55±0.03 E 0.11±0.01 0.14±0.01 0.08±0.01 0.06±0.01
下载: 导出CSV
-
[1] KAMINSKI T S, SCHELER O, GARSTECKI P. Droplet microfluidics for microbiology: techniques, applications and challenges[J]. Lab on a Chip, 2016, 16(12): 2168–2187. doi: 10.1039/c6lc00367b
[2] MAJUMDER S, WUBSHET N, LIU A P. Encapsulation of complex solutions using droplet microfluidics towards the synthesis of artificial cells[J]. Journal of Micromechanics and Microengineering, 2019, 29(8): 083001. doi: 10.1088/1361-6439/ab2377
[3] DING Y, HOWES P D, DEMELLO A J. Recent advances in droplet microfluidics[J]. Analytical Chemistry, 2020, 92(1): 132–149. doi: 10.1021/acs.analchem.9b05047
[4] VECCHIOLLA D, GIRI V, BISWAL S L. Bubble-bubble pinch-off in symmetric and asymmetric microfluidic expansion channels for ordered foam generation[J]. Soft Matter, 2018, 14(46): 9312–9325. doi: 10.1039/c8sm01285g
[5] YUAN D, ZHAO Q B, YAN S, et al. Recent progress of particle migration in viscoelastic fluids[J]. Lab on a Chip, 2018, 18(4): 551–567. doi: 10.1039/c7lc01076a
[6] LIU Z M, YANG Y, DU Y, et al. Advances in droplet-based microfluidic technology and its applications[J]. Chinese Journal of Analytical Chemistry, 2017, 45(2): 282–296. doi: 10.1016/S1872-2040(17)60994-0
[7] ZHU P G, WANG L Q. Passive and active droplet generation with microfluidics: a review[J]. Lab on a Chip, 2016, 17(1): 34–75. doi: 10.1039/c6lc01018k
[8] VLADISAVLJEVIĆ G T, KOBAYASHI I, NAKAJIMA M. Production of uniform droplets using membrane, microchannel and microfluidic emulsification devices[J]. Microfluidics and Nanofluidics, 2012, 13(1): 151–178. doi: 10.1007/s10404-012-0948-0
[9] MAZUTIS L, BARET J C, GRIFFITHS A D. A fast and efficient microfluidic system for highly selective one-to-one droplet fusion[J]. Lab on a Chip, 2009, 9(18): 2665–2672. doi: 10.1039/b903608c
[10] DENG X K, REN Y K, HOU L K, et al. Compound-droplet-pairs-filled hydrogel microfiber for electric-field-induced selective release[J]. Small, 2019, 15(42): 1903098. doi: 10.1002/smll.201903098
[11] 李战华, 吴健康, 胡国庆. 微流控芯片中的流体流动[M]. 北京: 科学出版社, 2012. LI Z H, WU J K, HU G Q. Fluid flow in microfluidic chips[M]. Beijing: Science Press, 2012.
[12] 陈晓东, 胡国庆. 微流控器件中的多相流动[J]. 力学进展, 2015, 45(1): 55–110. CHEN X D, HU G Q. Multiphase flow in microfluidic devices[J]. Advances in Mechanics, 2015, 45(1): 55–110.
[13] ROSTAMI B, MORINI G L. Experimental characterization of a micro cross-junction as generator of Newtonian and non-Newtonian droplets in silicone oil flow at low Capillary numbers[J]. Experimental Thermal and Fluid Science, 2019, 103: 191–200. doi: 10.1016/j.expthermflusci.2019.01.008
[14] ROSTAMI B, MORINI G L. Micro droplets of non-Newtonian solutions in silicone oil flow through a hydrophobic micro cross-junction[J]. Journal of Physics: Conference Series, 2017, 923: 012021. doi: 10.1088/1742-6596/923/1/012021
[15] FU T T, MA Y G, LI H Z. Breakup dynamics of slender droplet formation in shear-thinning fluids in flow-focusing devices[J]. Chemical Engineering Science, 2016, 144: 75–86. doi: 10.1016/j.ces.2015.12.031
[16] 刘赵淼, 杨洋. 几何构型对流动聚焦生成微液滴的影响[J]. 力学学报, 2016, 48(4): 867–876. DOI: 10.6052/0459-1879-16-063 LIU Z M, YANG Y. Influence of geometry configurations on the microdroplets in flow focusing microfluidics[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 867–876. doi: 10.6052/0459-1879-16-063
[17] MOON S K, CHEONG I W, CHOI S W. Effect of flow rates of the continuous phase on droplet size in dripping and jetting regimes in a simple fluidic device for coaxial flow[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2014, 454: 84–88. doi: 10.1016/j.colsurfa.2014.04.006
[18] TAN Y C, CRISTINI V, LEE A P. Monodispersed microfluidic droplet generation by shear focusing microfluidic device[J]. Sensors and Actuators B: Chemical, 2006, 114(1): 350–356. doi: 10.1016/j.snb.2005.06.008
[19] JOANICOT M, AJDARI A. Droplet control for microfluidics[J]. Science, 2005, 309(5736): 887–888. doi: 10.1126/science.1112615
[20] FATEHIFAR M, REVELL A, JABBARI M. Non-Newtonian droplet generation in a cross-junction microfluidic channel[J]. Polymers, 2021, 13(12): 1915. doi: 10.3390/polym13121915
[21] DU W, FU T T, DUAN Y F, et al. Breakup dynamics for droplet formation in shear-thinning fluids in a flow-focusing device[J]. Chemical Engineering Science, 2018, 176: 66–76. doi: 10.1016/j.ces.2017.10.019
[22] HARVIE D J E, DAVIDSON M R, COOPER-WHITE J J, et al. A parametric study of droplet deformation through a microfluidic contraction: shear thinning liquids[J]. International Journal of Multiphase Flow, 2007, 33(5): 545–556. doi: 10.1016/j.ijmultiphaseflow.2006.12.002
[23] DU W, FU T T, ZHANG Q D, et al. Self-similar breakup of viscoelastic thread for droplet formation in flow-focusing devices[J]. AIChE Journal, 2017, 63(11): 5196–5206. doi: 10.1002/aic.15834
[24] ARRATIA P E, GOLLUB J P, DURIAN D J. Polymeric filament thinning and breakup in microchannels[J]. Physical Review E, 2008, 77(3): 036309. doi: 10.1103/physreve.77.036309
[25] DERZSI L, KASPRZYK M, PLOG J P, et al. Flow focusing with viscoelastic liquids[J]. Physics of Fluids, 2013, 25(9): 092001. doi: 10.1063/1.4817995
[26] REN Y, LIU Z, SHUM H C. Breakup dynamics and dripping-to-jetting transition in a Newtonian/shear-thinning multiphase microsystem[J]. Lab on a Chip, 2015, 15(1): 121–134. doi: 10.1039/c4lc00798k
[27] KIM D Y, SHIM T S, KIM J M. Elastic effects of dilute polymer solution on bubble generation in a microfluidic flow-focusing channel[J]. Korea-Australia Rheology Journal, 2017, 29(2): 147–153. doi: 10.1007/s13367-017-0016-0
[28] SHI Y, TANG G H. Lattice boltzmann simulation of droplet formation in non-Newtonian fluids[J]. Communications in Computational Physics, 2015, 17(4): 1056–1072. doi: 10.4208/cicp.2014.m333
[29] XUE C D, SUN Z P, LI Y J, et al. Non-Newtonian droplet generation in a flow-focusing microchannel[C]//Proceedings of ASME 2019 6th International Conference on Micro/Nanoscale Heat and Mass Transfer, Dalian, China. 2019. doi: 10.1115/MNHMT2019-4196
[30] YASUDA K, ARMSTRONG R C, COHEN R E. Shear flow properties of concentrated solutions of linear and star branched polystyrenes[J]. Rheologica Acta, 1981, 20(2): 163–178. doi:
[31] LI D, XUAN X C. Fluid rheological effects on particle migration in a straight rectangular microchannel[J]. Microfluidics and Nanofluidics, 2018, 22(4): 1–10. doi: 10.1007/s10404-018-2070-4
[32] BHAT P P, APPATHURAI S, HARRIS M T, et al. Formation of beads-on-a-string structures during break-up of viscoelastic filaments[J]. Nature Physics, 2010, 6(8): 625–631. doi: 10.1038/nphys1682
[33] OLIVEIRA M S N, MCKINLEY G H. Iterated stretching and multiple beads-on-a-string phenomena in dilute solutions of highly extensible flexible polymers[J]. Physics of Fluids, 2005, 17(7): 071704. doi: 10.1063/1.1949197
[34] ZHOU C F, YUE P T, FENG J J. Formation of simple and compound drops in microfluidic devices[J]. Physics of Fluids, 2006, 18(9): 092105. doi: 10.1063/1.2353116
[35] XUE C D, CHEN X D, LI Y J, et al. Breakup dynamics of semi-dilute polymer solutions in a microfluidic flow-focusing device[J]. Micromachines, 2020, 11(4): 406. doi: 10.3390/mi11040406
[36] ROUMPEA E, CHINAUD M, ANGELI P. Experimental investigations of non-Newtonian/Newtonian liquid-liquid flows in microchannels[J]. AIChE Journal, 2017, 63(8): 3599–3609. doi: 10.1002/aic.15704
[37] HONG J S, COOPER-WHITE J. Drop formation of Carbopol dispersions displaying yield stress, shear thinning and elastic properties in a flow-focusing microfluidic channe[J]. Korea-Australia Rheology Journal, 2009, 21(4): 269–280.
-
期刊类型引用(2)
1. 梁定新，吕鑫钰，覃开蓉，薛春东. 基于非牛顿微液滴的粒子封装及检测. 力学学报. 2024(05): 1307-1316 . 
百度学术
2. 邢雷，綦航，蒋明虎，张爽，韩国鑫，关帅. T型微通道入口角度对剪切变稀流体微液滴制备影响. 高校化学工程学报. 2024(03): 422-431 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 328
- HTML全文浏览量: 169
- PDF下载量: 66
- 被引次数: 4
