0   引言

固定翼飞机飞行过程中，其上下翼面存在压力差，使得气流在机翼两侧翼尖处强烈翻卷形成一对反向旋转的尾涡，即翼尖涡。翼尖涡是飞机尾流中主要的相干结构，在无外加干扰的情况下，翼尖涡的强度在100倍机翼展长范围内不会发生明显的衰减，其携带的旋转能量会引起作用范围内后方飞机的飞行速度、高度、航向、滚转角及其他飞行特性发生显著变化，影响其飞行安全，由此制定的飞机尾流安全标准决定了飞机起降频率、影响机场运营效率^[1-2]。对翼尖涡尾流场及其相关统计参数进行深入研究，进而发展促使尾涡失稳耗散的流动控制技术具有重要的应用价值。

通常，根据实验观测平面到机翼后缘距离的不同，将翼尖涡尾流场分为近场(x/b≤10，x为观测平面到机翼后缘的水平距离，b为机翼展长)、中远场(10 < x/b≤100)和耗散场(x/b>100)。目前，对于翼尖涡尾流场的实验研究，主要采用热线风速仪和多孔探针等空间单点测速系统在风洞中对尾流场进行速度场测量，进而分析旋涡的统计参数^[3-4]。一方面，接触式测量对原有流场的干扰无法消除，更不利的因素在于，翼尖涡在受到扰动之后会呈现显著的非定常性，涡核位置呈不规则摆动状态^[5-7]，涡核大小也不固定，单点测速系统无法得到瞬时流场的全貌；另一方面，由于风洞实验段长度的限制，无法对翼尖涡发展的中远场进行有效测量。为此，本研究采用二维粒子图像测速技术(2DPIV)在水洞中对翼尖涡尾流场进行长时间的统计观测，测量区域覆盖翼尖涡发展的中远场。

已有的研究表明^[8-11]，反向旋转的翼尖涡从机翼后缘脱落后，受到扰动之后会产生不稳定运动，涡核中心会呈现出类似正弦的不稳定波动，这种不稳定运动称为“Vortex Wandering”^[9]。而且随着涡对向下游发展，不稳定运动的振幅会逐渐增大。翼尖涡涡核中心在流场中的位置并不固定，简单地对速度场采用时间平均的方法(temporal average)来提取数据会导致翼尖涡统计参数存在较大的误差^[9-11]。针对涡对不稳定运动导致旋涡统计参数失真的情况，本文采用涡核中心对齐平均(re-centered average)的方法，屏蔽掉涡对不稳定运动对于旋涡统计参数的影响，提高统计参数的准确度，并定量化给出低雷诺数下翼尖涡涡核半径、涡量峰值随流向站位的变动规律。本文对翼尖涡统计参数的研究可为翼尖涡尾流场的数值计算以及翼尖涡控制技术提供参考。

1   实验模型和设备

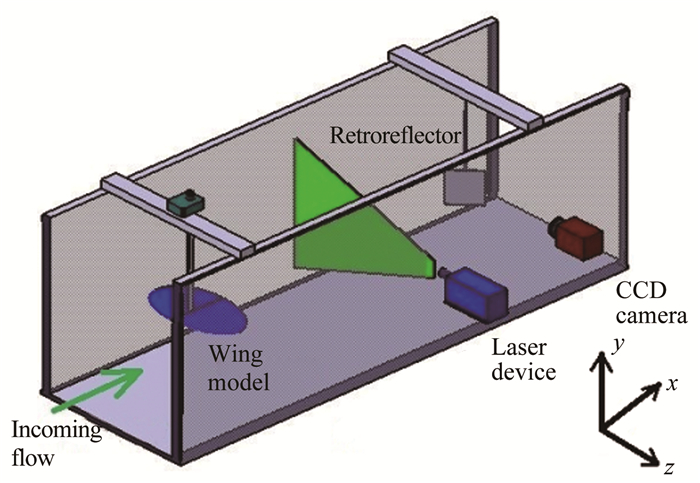
实验在北京航空航天大学低速回流式水洞中进行。该水洞实验段长12 m，横截面为1.2 m×1.0 m。水洞自由来流速度V_∞可在0~50 cm/s的范围内无级调节, 实验段湍流度不超过0.8%。该水洞进行过大量条带稳定性方面的实验研究，流场品质满足旋涡稳定性实验要求^[12-13]。实验模型为三维椭圆机翼，如图 1所示，机翼截面为低雷诺数翼型E387，展长b=12 cm，翼根弦长c=7 cm。机翼模型由3D打印制作，表面进行了抛光处理。实验装置如图 2所示，其中x, y, z方向分别代表流向、法向和展向，以模型翼根弦长后缘作为坐标原点。模型通过连接杆固连在迎角机构上，机翼迎角可在-20°~20°范围内调整。

图  1  椭圆机翼模型

Fig.  1  Elliptical wing model

下载: 全尺寸图片 幻灯片

图  2  实验装置示意图

Fig.  2  Schematic of the experimental setup

下载: 全尺寸图片 幻灯片

进行PIV实验时，流场中布撒平均粒径为20 μm的空心玻璃微珠作为示踪粒子，密度为1.05 g/mm³，低速情况下粒子跟随性良好^[14-15]。激光片光由1台500 mJ双曝光脉冲激光器提供，片光厚度约为1 mm，波长为532 nm，片光下游60 cm处竖直安装光学平面镜反射粒子图像，分辨率为2456 pixel×2058 pixel的CCD相机接收平面镜反射光并记录图像。PIV实验前，采用染色液法定性观测了平面镜对周围流场区域的扰动，流动显示的结果表明平面镜的存在不会对上游片光区域翼尖涡的稳定性产生影响。相机和激光之间通过同步器(北京立方天地SM-MicroPulse725)进行控制。实验中相机视野范围为17 cm×15 cm(y-z平面)，空间分辨率约为14 pixel/mm。

本实验中，通过改变激光片光距离模型后缘的位置，对翼尖涡尾流场进行了10个流向站位(x/b=1.0, 1.5, 2.5, 4.5, 6.5, 9.5, 14.5, 19.5, 27.5, 35.5)的观测，覆盖翼尖涡发展的近场和中远场。在每个流向站位，进行4个迎角(α=2°, 4°, 6°, 8°)的测量，自由来流速度为10 cm/s，基于平均气动弦长的雷诺数约为5500。

在模型区下游每一流向站位，相机记录1500对粒子图像，采集频率为7 Hz。在PIV图像处理技术上，本文采用多步迭代的Lucas-Kanade光流法(简称L-K算法)，相比于传统基于互相关的PIV算法，L-K算法提高了计算效率和精度，而且获得了更为光滑的速度场^[16-17]。

2   翼尖涡相关参数定义

涡量用来表示流体微团旋转运动的快慢，定义顺时针旋转涡量为正。实验中测量的是y-z平面内的翼尖涡周向速度，通过式(1)可得到翼尖涡轴向涡量分布:

环量通常被作为衡量翼尖涡衰减的能量指标，可表示成涡量的面积分：

识别涡核中心通常有3种方法：(1)旋涡旋转的周向速度和径向速度均为0的点；(2)涡量峰值所在的空间点；(3)涡量权重中心。对于定常流动，3种方法统计出来的涡核中心的空间位置理论上应该重合^[18]。考虑到实验中存在扰动，翼尖涡的空间运动呈现强的三维性，涡核中心存在对流运动，速度为0的点和通过涡量峰值求解出来的涡核中心存在一定差异。对不稳定非定常运动旋涡中心的辨识，方法(1)和(2)并不适用。本文采用方法(3)确定涡核中心，涡核中心坐标(z_c, y_c)由式(3)和(4)给出^[19]：

涡核半径r_c由式(5)给出^[19]：

3   实验结果及分析

3.1   Temporal average和re-centered average对比

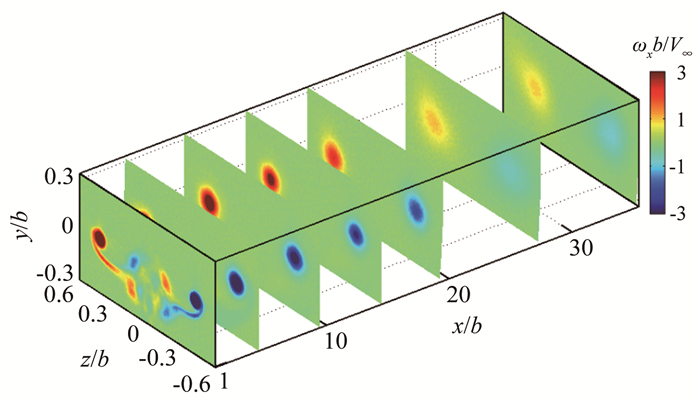
图 3给出了迎角6°，速度10 cm/s时翼尖涡平均涡量场沿流向站位的变化(涡量ω_x利用式ω_xb/V_∞无量纲化)。翼尖涡在近尾迹区(图 3中x/b=1处)，涡量分布较为集中。2个涡中心处脱落出方向相反、反对称分布的小旋涡结构，这些结构来自于机翼后缘分离的尾迹以及流体流经支撑杆与机翼连接处产生的涡系。由于翼尖涡强的卷携作用，随着旋涡向下游发展，中间区域小的涡结构逐渐与两侧翼尖涡发生融合，在9.5倍展长处，已基本观测不到中间区域的涡结构。翼尖涡向下游发展过程中，涡量分布逐渐分散。

图  3  翼尖涡平均涡量场沿流向站位分布，α=6°

Fig.  3  Variation of the mean vorticity along stream-wise position at α=6°

下载: 全尺寸图片 幻灯片

反向旋转的涡对受到扰动后，在相互诱导的作用下，涡对在三维空间会呈现出不稳定运动，随着涡管向流场下游发展，其不稳定运动幅度逐渐变大^{[1, 6]}。根据不稳定运动波长的不同，研究者将反向旋转涡对的不稳定运动分为长波不稳定和短波不稳定^{[1, 8]}。这种长波和短波的不稳定运动在水洞流动显示实验和真实的飞机翼尖涡尾迹中很容易观测到^[10]。

由于涡对的运动，涡核中心在空间的位置并不固定，直接采用未修正的速度场数据进行时间平均(temporal average)来提取旋涡统计参数会导致数据失真，例如旋涡切向速度减小、涡核半径变大、雷诺应力和速度脉动增大等。本文分析中，采用涡核中心对齐平均的方法(re-centered average)提取翼尖涡的相关参数。具体方法为：首先，利用式(3)和(4)，根据每一瞬时的速度场确定涡核中心的空间位置坐标，为保证叠加求平均的速度场矩阵的维度相同，以瞬时的涡心位置为中心提取100 vector×100 vector区域的速度场数据，然后在时间维度上对截取的1500个速度场进行叠加平均，最后以得到的平均涡量场计算涡核半径、切向速度和涡量峰值。Re-centered average方法可屏蔽掉旋涡的不稳定运动对翼尖涡统计参数造成的不利影响。

图 4给出了3个迎角下、流向站位x/b=9.5时temporal average和re-centered average方法统计得到的平均涡量场对比。图中第一列为temporal average方法得到的涡量结果, 第二列为re-centered average方法得到的涡量结果, 第三列给出了2种方法得到的过涡核中心涡量分布的对比。从图中可以看出, re-centered average方法得到的平均涡量明显大于temporal average的结果，涡量分布更加集中。涡对在流场中的不稳定运动会导致涡量分布更加分散，涡量峰值降低。从第三列图像可以看出，翼尖涡过涡核中心的涡量分布符合高斯分布。随着迎角的增大，2种方法得到的峰值涡量差别有减小的趋势。

图  4  Temporal average和re-centered average方法统计得到的平均涡量场对比(x/b=9.5)

Fig.  4  Comparison of mean vorticity obtained by temporal average and re-centered average methods at stream-wise location x/b=9.5

下载: 全尺寸图片 幻灯片

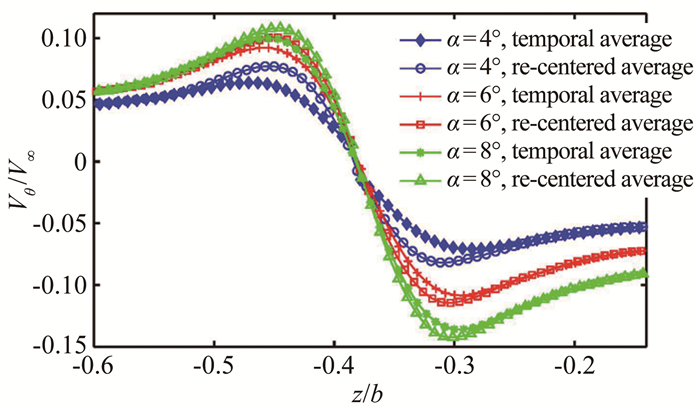
图 5给出了与图 4相同实验工况下temporal average和re-centered average方法统计得到的过涡核中心旋涡切向速度V_θ分布对比。旋涡旋转的切向速度存在2个速度峰值点，由于涡对相互诱导的下洗作用，对于左翼涡，涡核右侧的速度峰值明显大于左侧。切向速度随迎角增大而增大。Re-centered average方法得到的切向速度大于temporal average方法的结果。随着迎角增大，2种方法的差值逐渐减小。

图  5  Temporal average和re-centered average方法统计得到的切向速度分布对比，x/b=9.5

Fig.  5  Comparison of tangential velocity obtained by temporal average and re-centered average methods at stream-wise location x/b=9.5

下载: 全尺寸图片 幻灯片

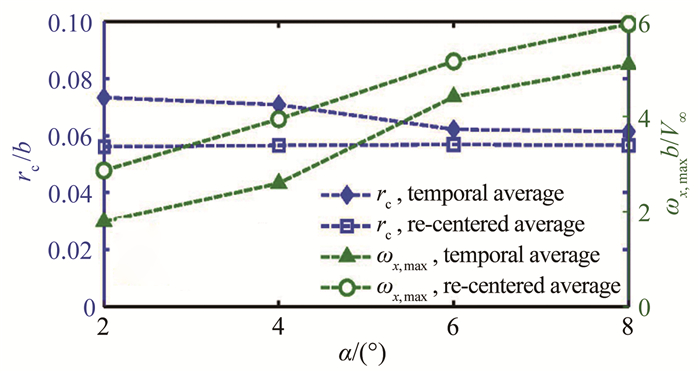
图 6给出了temporal average和re-centered average方法统计得到的涡核半径r_c和涡量峰值ω_{x, max}对比。Re-centered average得到的涡核半径更小，涡量峰值更大。在当前实验工况下，涡核半径最大不超过机翼展长的8%，而且几乎不随迎角发生变化，即翼尖涡涡核尺寸并不随旋涡强度而发生变化。涡量峰值随迎角增大而增大。

图  6  Temporal average和re-centered average方法统计得到的涡核半径和涡量峰值对比，x/b=9.5

Fig.  6  Comparison of vortex core radius and the peak vorticity obtained by temporal average and re-centered average methods at stream-wise location x/b=9.5

下载: 全尺寸图片 幻灯片

图 7给出了temporal average和re-centered average方法统计得到的切向速度峰值、涡核半径和涡量峰值相对误差, 其定义如下：

图  7  Temporal average和re-centered average方法统计的切向速度峰值、涡核半径和涡量峰值相对误差，x/b=9.5

Fig.  7  Relative difference of the peak tangential velocity, vortex core radius and peak vorticity obtained by temporal average and re-centered average methods at stream-wise location x/b=9.5

下载: 全尺寸图片 幻灯片

式中, 下标T和R分别代表temporal average和re-centered average方法统计得到的结果。可以看出，3个统计参数中，涡量峰值相对误差最大，2°迎角时可达37.1%，切向速度相对误差最小。随着迎角增大，2种方法得到的3个统计参数的相对误差逐渐减小，表明涡对的不稳定运动振幅减小。机翼迎角与翼尖涡强度直接相关，迎角越大，机翼上下翼面压强差越大，翼尖涡强度越大。由此可以推断，旋涡强度越大，旋涡不稳定运动的振幅越小，涡对抵抗扰动的能力越强。

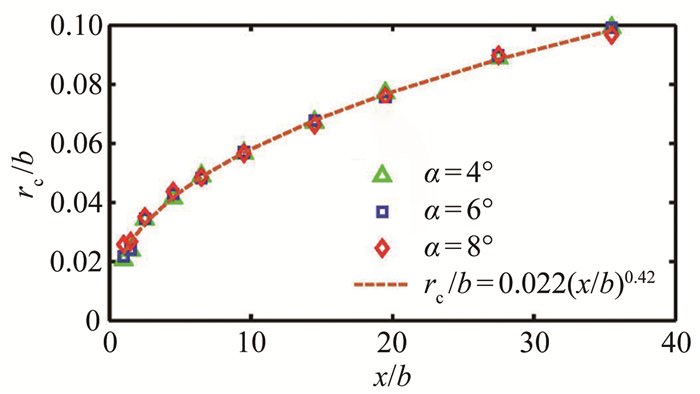
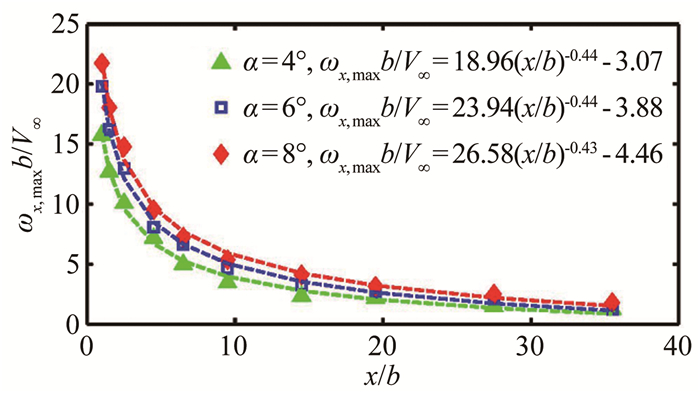
3.2   涡核半径和涡量峰值统计分析

涡核半径和涡量峰值是描述翼尖涡特性的2个重要参数，涡核半径表征旋涡对周围流场的影响范围，涡量峰值则间接表征旋涡的强度。采用re-centered average方法统计翼尖涡涡核半径和涡量峰值沿流向站位的变化规律。图 8和9分别给出了3个迎角下，涡核半径和涡量峰值随流向站位的变化，图中虚线为幂函数拟合的结果。随着涡对向下游发展，由于涡量的扩散，涡核半径逐渐膨胀，涡量峰值迅速衰减，但是增长/衰减速度逐渐减小。在相同的流向站位，涡核半径几乎不随迎角而改变(与图 6所得结论一致)。从图 9可以看出，随着迎角增大，幂函数的系数逐渐增大，涡量峰值衰减的速率随迎角增大而增大。

图  8  涡核半径随流向站位的变化

Fig.  8  Variation of the vortex radius with respect to the stream-wise location

下载: 全尺寸图片 幻灯片

图  9  涡量峰值随流向站位的变化

Fig.  9  Variation of the peak vorticity with respect to the stream-wise location

下载: 全尺寸图片 幻灯片

4   结论

通过水洞试验，采用2DPIV技术对垂直于流向的翼尖涡截面流场进行了实验测量，给出了temporal average和re-centered average方法提取翼尖涡统计参数的定量化对比，最后统计了低雷诺数下翼尖涡涡核半径和涡量峰值随流向站位的变化规律，从侧面反映了涡对向下游发展的三维流动特性。研究结果表明：

(1) 本实验研究的雷诺数下，由于涡对的不稳定运动，temporal average和re-centered average方法提取的涡量峰值相对误差最大可达37.1%。由于涡对在流场中的不稳定摆动，直接采用涡量平均方法会导致涡量峰值和切向最大速度减小，涡核半径增大。随着迎角增大，2种方法统计的涡量峰值、涡核半径、切向速度相对误差逐渐减小。由此可推断：涡对不稳定运动的振幅随涡强度的增大而逐渐减小，涡对抵抗扰动的能力增强。

(2) 由于涡量的扩散作用，涡核半径随流向站位逐渐增大；涡量峰值随流向站位迅速减小。涡核半径和涡量峰值随流向站位分别呈现出近似符合幂函数的增长和衰减规律，增长/衰减速率随流向站位的增大而逐渐减缓。

(3) 对飞机尾流场进行干扰、促使飞机翼尖涡对能量提前耗散的流动控制技术得以有效实施的重要前提是准确获取翼尖涡尾流场特性。例如，翼尖喷流主动流动控制技术，其喷流系数、喷流方向、喷口形状、喷口位置的选择均需要准确获知尾涡中的流动结构^[20-21]。本文提供了一种更为准确的时均分离尾涡流场的分析方法，相对于直接将PIV求得的尾涡流场进行时间平均，可以得到更精准的流场参数。通过re-centered average方法提取涡对的统计参数沿流向站位的变化特性也可对数值计算结果进行校核验证。